1. Необходимо проложить железнодорожный путь из левой нижней вершины (А) в правую верхнюю (В) (найти кратчайший путь) если стоимость прокладки на отдельных участках дана в прямоугольном взвешенном графе.

Веса по оси Х: 96752 18981 83698 87982 86386 86878

Веса по оси У: 37173 82593 85978 12596 87396 81878

; 27; 7; 43; 10; 0,5.

Пошаговое объяснение:

Для начала превратим смешанные числа в неправильные дроби. Для этого нужно целую часть умножить на знаменатель и прибавить к результату числитель. Знаменатель при этом не изменяется, а полученный результат идёт в числитель.

Теперь приведём дроби к общему знаменателю. Общий знаменатель — такое число, на которое делится знаменатель каждой дроби. В данном случае 15 делится на 5, поэтому 15 и будщет общим знаменателем. Ту дробь, у которой в знаменателе пять, мы домножаем на три: умножается и числитель, и знаменатель. Та дробь, у которой в знаменателе 15, не изменяется.

Остальные примеры решаются аналогично.

б)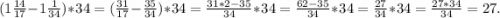

в)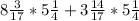 . Здесь имеет смысл 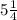вынести за скобки. Тогда получается: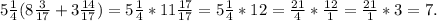

г)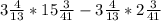 . Здесь аналогично.

д)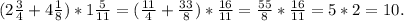

е)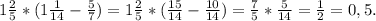

P. S. Сделано допущение, что в г) дробь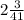 , а не 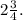В противном случае решается тяжело.

78,884

Пошаговое объяснение:

Для решения данной задачи воспользуемся теоремой синусов. Звучит она так: "Стороны треугольника пропорциональны синусам противолежащих углов.", а выглядит так:

, где a, b, с - стороны треугольника, а sin(a,b,с) - противолежащие углы соответствующих сторон треугольника.

Подставим известные нам значения, а сторону NK возьмем за x :

По таблице Брадиса подставляем вместо синусов - числовые значения. Получаем:

Точное значение получить невозможно, но приближенная длина стороны NK = 78,884

Для наглядности моего решения - прикрепил фото с пояснением.