35. Отдельные участки моря находятся под наблюдение специальных приборов, которые называются радарами. Каждое судно, поподающее в зону работы радара фиксируется светлой точкой на экране.
По координатам этой точки, можно определить истинное расположение судна в открытом море.
Выполните вычисления и найдите координаты точек. Отметьте точками положение судов на
экране радара:
Парусник: Р(х; у):
х = (-2) - (-2) - 3=
у з
(-24) =
PC
Линкор: L(x, y):
І, = (-3 – 4)-(3 - 4) =
у = (-5) - 31 =
L(
в 3 номере под а):
показатели корней разные (12 и 6), мы можем получить одинаковые, умножив показатель 6 на 2, поэтому и подкоренное выражение домножаем на 2:
было: √6ой степени из 5⁵, стало: √12ой степени из 5¹⁰
то же самое в номере 3 под б):
показатели корней разные (квадратный корень из 3 и кубический корень из 9), мы можем получить одинаковые, домножив квадратный корень на 3 (чтобы получить 6) и кубический корень на 2 (чтобы получить 6), поэтому и подкоренные выражения домножаем на 2:
было: √2ой степени из 3, стало: √6ой степени из 3³ и второй множитель: было: √3ей степени из 9, стало: √6ой степени из 9²
Дифференцируем первое уравнение:
Подставим выражение для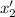 :
:
Домножим первое уравнение системы на 6 и сложим его с полученным уравнением:
Составим однородное уравнение, соответствующее данному неоднородному:
Составим характеристическое уравнение:
Общее решение однородного уравнения:
Частно решение неоднородного уравнения ищем в виде:
Найдем первую и вторую производную:
Подставим в неоднородное уравнение:
Частное решение неоднородного уравнения:
Общее решение неоднородного уравнения:
Найдем первую производную:
Выразим из первого уравнения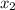 :
:
Общее решение системы: