4. Решите задачу с диаграммы Эйлера-Венна: 35 учеников зарегистрировано или городской библиотсках. Из них 25 регулярно посещают школьную библиотеку, а 20 городскую.
Сколько учеников:
а) Посещают обе библиотеки?
b) Не посещают городскую библиотеку?
c) Не посешают школьную библиотеку?
d) Ходят только в школьную библиотеку?
ответьте на все вопросы
1)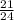 ,
, 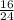
2)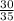 ,
, 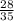
3)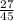 ,
, 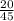
4)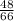 ,
, 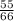
5)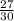 ,
, 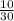
6)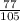 ,
, 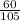
7)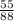 ,
, 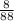
8)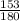 ,
, 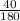
Пошаговое объяснение:
1)
НОК (8 ; 3) = 24.
Так как 24 : 8 = 3, мы домножаем числитель и знаменатель первой дроби на 3.
Так как 24 : 3 = 8, мы домножаем числитель и знаменатель второй дроби на 8.
ответ: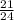 ,
, 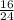 .
.
2)
НОК (7 ; 5) = 35.
Так как 35 : 7 = 5, мы домножаем числитель и знаменатель первой дроби на 5.
Так как 35 : 5 = 7, мы домножаем числитель и знаменатель второй дроби на 7.
ответ: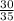 ,
, 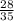 .
.
3)
НОК (5 ; 9) = 45.
Так как 45 : 5 = 9, мы домножаем числитель и знаменатель первой дроби на 9.
Так как 45 : 9 = 5, мы домножаем числитель и знаменатель второй дроби на 5.
ответ: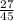 ,
, 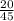 .
.
4)
НОК (11 ; 6) = 66.
Так как 66 : 11 = 6, мы домножаем числитель и знаменатель первой дроби на 6.
Так как 66 : 6 = 11, мы домножаем числитель и знаменатель второй дроби на 11.
ответ: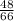 ,
, 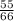 .
.
5)
НОК (10 ; 3) = 30.
Так как 30 : 10 = 3, мы домножаем числитель и знаменатель первой дроби на 3.
Так как 30 : 3 = 10, мы домножаем числитель и знаменатель второй дроби на 10.
ответ: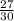 ,
, 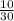 .
.
6)
НОК (15 ; 7) = 105.
Так как 105 : 15 = 7, мы домножаем числитель и знаменатель первой дроби на 7.
Так как 105 : 7 = 15, мы домножаем числитель и знаменатель второй дроби на 15.
ответ: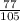 ,
, 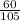 .
.
7)
НОК (8 ; 11) = 88.
Так как 88 : 8 = 11, мы домножаем числитель и знаменатель первой дроби на 11.
Так как 88 : 11 = 8, мы домножаем числитель и знаменатель второй дроби на 8.
ответ: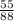 ,
, 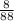 .
.
8)
НОК (20 ; 9) = 180.
Так как 180 : 20 = 9, мы домножаем числитель и знаменатель первой дроби на 9.
Так как 180 : 9 = 20, мы домножаем числитель и знаменатель второй дроби на 20.
ответ: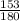 ,
, 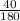 .
.
1)xy-2y = y(x-2)
2)16a^2-81 = (4a)^2-9^2 = (4a-9)(4a+9)
3)3x^2-6x^3 = 3x^2(1-2x)
4)x^2-10x+25 = (x-5)^2
5)3(x-1)+y(x-1) = (3+y)(x-1)
6)2a^2-4ab+2b^2 = 2(a^2-2ab+b^2) = 2(a-b)^2
Пошаговое объяснение:
В 1, 3, 5 и 6 выносится общий множитель за скобки.
Во 2 применяется формула сокращенного умножения для разности квадратов. Разность квадратов двух выражений равна произведению разности этих выражений на их сумму.
В 4 и 6 применяется формула сокращенного умножения для квадрата разности. Квадрат разности двух выражений равен квадрату первого, минус удвоенное произведение первого и второго, плюс квадрат второго.