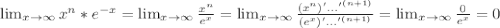Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
анр5гн5р5рррр
24.11.2021 22:33 •
Математика
50 ! вычислить пределы с правила лопиталя:
1) lim 1-cos ax/1-cos bx
x --> 0
2) lim x ^n *e ^-x
x--> 00( бесконечность)
Показать ответ
Ответ:
AlenaSmaychkov222
17.08.2020 15:01
1)
2)
0,0
(0 оценок)
Популярные вопросы: Математика
arturpushkin202453
22.02.2023 15:42
В трёх классах 170учеников.В двух одинаково,а в третьем на 5 уч.меньше....
Марс2014
09.03.2021 11:01
х - 3,73/5 + 2х - 1,86/10 4...
Lenaaaa111
19.06.2022 03:30
Какой знак будет -) -) -) -) -) -2...
Alena18091
08.06.2021 11:07
Решите примеры в столбик....
АртурЗезарахов
12.03.2022 05:20
5. Вычисли письменно. а) 421 : 2 314 : 2765 - 45б) 963 : 3 842:2 87 + 653в) 64:2424 : 2770 - 659321 : 3488 : 4684 : 2...
Артерия
17.04.2021 02:23
NellyouPolo- ribunach10,8x+19,460 2 = 1928x Of+ 19, 4x 20, &x 20 d 0,2x = 40,41084044 19,4...
Срочноооооопжлст
15.07.2021 02:35
Укажіть кількість натуральних чисел, менших від кореня рівняння (10,63 +х) - 3,63= 12,89....
sdfdsgdfh
28.09.2021 04:49
В школе французский язык изучают 127 учащихся, что составляет 20% от числа всех учащихся. Сколько учащихся в школе?...
evamakarova20
01.11.2021 11:01
Измерьте длину и ширину стола в комнате и найдите его периметр...
69TanyaKoT69myr
05.08.2021 02:46
Розклади на множники (t10+u10)2−(t10−u10)2−t2u2...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
1)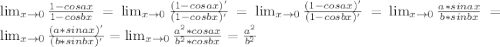
2)