Определение. Назовём числом сочетаний из n по k число выбрать из множества мощностью n элементов множество мощностью k элементов, будем обозначать и определим формулой
Если нужно доказательство, пишите
Итак, приступаем к решению.
Сначала раздаем первому игроку.
Для него есть 32 карты, из которых мы выбираем 10. Тогда количество выбрать эти карты есть число сочетаний из 32 по 10.
Но можно было просто оставить
Мы уже дали 10 карт первому, поэтому осталось 32 - 10 = 22 карт.
Тогда количество раздать второму 10 карт из 22 - это
Или опять же можно было бы оставить
Третьему останется всего лишь 22 - 10 = 12 карт. Тогда точно также, число выбрать из 12 карт 10 равно
Ну хоть здесь нормальное число. Но опять же можно было и оставить
И так, для каждого из игроков есть свои варианты выбора, причем выбор другого, напрямую зависит от выбрав первого. Тогда нам необходимо перемножить все эти результаты.
или
Пошаговое объяснение:
Давайте сначала введём понятие.
Определение. Назовём числом сочетаний из n по k число выбрать из множества мощностью n элементов множество мощностью k элементов, будем обозначать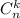
и определим формулой
Если нужно доказательство, пишите
Итак, приступаем к решению.
Сначала раздаем первому игроку.
Для него есть 32 карты, из которых мы выбираем 10. Тогда количество выбрать эти карты есть число сочетаний из 32 по 10.
Но можно было просто оставить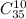
Мы уже дали 10 карт первому, поэтому осталось 32 - 10 = 22 карт.
Тогда количество раздать второму 10 карт из 22 - это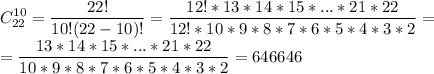
Или опять же можно было бы оставить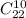
Третьему останется всего лишь 22 - 10 = 12 карт. Тогда точно также, число выбрать из 12 карт 10 равно
Ну хоть здесь нормальное число. Но опять же можно было и оставить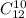
И так, для каждого из игроков есть свои варианты выбора, причем выбор другого, напрямую зависит от выбрав первого. Тогда нам необходимо перемножить все эти результаты.
Получим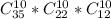
Или если в числах, то это
6.12(б)
log₈₁x+log₉(x)+log₃x=7
ОДЗ х>0,
по правилу перехода к новому основанию перейдем к основанию 3
log₃x/log₃81+log₃x/log₃9+log₃x=7; приведем к общему знаменателю и воспользуемся определением логарифма.
log₃x/4+log₃x/2+log₃x=7
7*log₃x=28
log₃x=4; х=81∈ОДЗ.
x=81
6.13(б)
log₃x+2*log₉x*log₂₇x+4*log₈₁x=8
ОДЗ х∈(0;+∞), на этом множестве можно упростить уравнение.
log³x+2*0.5*log₃x+3*(1/3)*log₃x+4*(1/4)*log₃x=8
log₃x=8/4
log₃x=2
x=3²
x=9∈ОДЗ
х=9
6.15(а)
log²₂x+(5/2)(log₂x/log₂3)* log₂x+ (log²₂х)/log²₂3 =0
log²₂x*(1+(5/(2log₂3) +1/log²₂3 )=0
(1+(5/(2log₂3) +1/log²₂3 )≠0
log²₂x=0
log₂x=0
х=2⁰
x=1∈ОДЗ
х=1