Артем нарвав у лісі горіхів. По дорозі додому він зустрів одного за одним чотирьох друзів і кожному віддав половину тих горіхів, що були в нього. Додому він приніс 10 горіхів. Скільки горіхів було в Артема спочатку? 170 760 10лв
Так как угол ADC равен π/3, то есть 60°, и DE - биссектриса угла ADC, то углы ADE и CDE равны по 60°:2=30°.
Сумма смежных углов параллелограмма равна 180°, значит:
∠BCD=180°-∠ADC=180°-60°=120°
Так как угол BCD равен 120° и CE - биссектриса угла BCD, то углы BCE и DCE равны по 120°:2=60°.
Рассмотрим треугольник CDE. Так как два угла в нем известны, то найдем третий угол CED:
∠CED=180°-∠CDE-∠DCE=180°-30°-60°=90°
Значит, треугольник CDE - прямоугольный.
В прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы.
Введем обозначения. Пусть катет CE, лежащий против угла в 30°, равен a. Тогда гипотенуза CD равна 2а. Заметим, что CD соответствует одной из сторон параллелограмма.
Рассмотрим треугольник ВСЕ. Найдем неизвестные его углы.
Так как противоположные углы параллелограмма равны, то:
∠ABC=∠ADC=60°
Зная два угла треугольника, найдем третий:
∠BEC=180°-∠BCE-∠CBE=180°-60°-60°=60°
Все углы треугольника ВСЕ равны, значит он - равносторонний.
Одна из сторон треугольника ВСЕ обозначена как а, значит и все его стороны равны а. В том числе, сторона параллелограмма ВС=а.
Таким образом, известны в наших обозначениях стороны параллелограмма: AB=DC=2a, BC=AD=a.
Рассмотрим треугольник АВС. Запишем для него теорему косинусов:
Подставим известные соотношения:
По условию АС=3.
(отрицательный корень смысла не имеет)
Вернемся к треугольнику CDE. Две стороны в нем теперь известны: , . Запишем теорему Пифагора:
Сторого не суди, информация взята из интернета Ведущим положением в научной и практической деятельности парка является - сохранение уникального природного и историко-культурного комплекса для устойчивого развития.
C 2001 года Национальный биосферный парк «Водлозерский» входит во Всемирную сеть биосферных резерватов ЮНЕСКО. В связи с этим фактом, парк выполняет три основные функции, характерные для биосферных резерватов мира:
- сохранение – вклад в сохранение ландшафтов, экосистем, видов и генофонда;
- развитие – поощряющее экономическое и общественное развитие, обеспечивающее социально-культурную и экологическую стабильность;
- поддержка целевых исследований – показательных проектов, экологического воспитания, исследований и мониторинга локального, регионального, национального и планетарного уровня по сохранению среды и устойчивому развитию.
Организация и проведение исследований природы и культурного наследия осуществляется усилиями сотрудников научного отдела, а также учеными из КарНЦ РАН, ПетрГУ, других вузов страны. С некоторыми из них у Парка установились продолжительные и результативные научные и дружественные связи.
Так как угол ADC равен π/3, то есть 60°, и DE - биссектриса угла ADC, то углы ADE и CDE равны по 60°:2=30°.
Сумма смежных углов параллелограмма равна 180°, значит:
∠BCD=180°-∠ADC=180°-60°=120°
Так как угол BCD равен 120° и CE - биссектриса угла BCD, то углы BCE и DCE равны по 120°:2=60°.
Рассмотрим треугольник CDE. Так как два угла в нем известны, то найдем третий угол CED:
∠CED=180°-∠CDE-∠DCE=180°-30°-60°=90°
Значит, треугольник CDE - прямоугольный.
В прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы.
Введем обозначения. Пусть катет CE, лежащий против угла в 30°, равен a. Тогда гипотенуза CD равна 2а. Заметим, что CD соответствует одной из сторон параллелограмма.
Рассмотрим треугольник ВСЕ. Найдем неизвестные его углы.
Так как противоположные углы параллелограмма равны, то:
∠ABC=∠ADC=60°
Зная два угла треугольника, найдем третий:
∠BEC=180°-∠BCE-∠CBE=180°-60°-60°=60°
Все углы треугольника ВСЕ равны, значит он - равносторонний.
Одна из сторон треугольника ВСЕ обозначена как а, значит и все его стороны равны а. В том числе, сторона параллелограмма ВС=а.
Таким образом, известны в наших обозначениях стороны параллелограмма: AB=DC=2a, BC=AD=a.
Рассмотрим треугольник АВС. Запишем для него теорему косинусов:
Подставим известные соотношения:
По условию АС=3.
Вернемся к треугольнику CDE. Две стороны в нем теперь известны: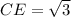 ,
, 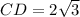 . Запишем теорему Пифагора:
. Запишем теорему Пифагора:
Выражаем искомый отрезок DE:
ответ: 3
C 2001 года Национальный биосферный парк «Водлозерский» входит во Всемирную сеть биосферных резерватов ЮНЕСКО. В связи с этим фактом, парк выполняет три основные функции, характерные для биосферных резерватов мира:
- сохранение – вклад в сохранение ландшафтов, экосистем, видов и генофонда;
- развитие – поощряющее экономическое и общественное развитие, обеспечивающее социально-культурную и экологическую стабильность;
- поддержка целевых исследований – показательных проектов, экологического воспитания, исследований и мониторинга локального, регионального, национального и планетарного уровня по сохранению среды и устойчивому развитию.
Организация и проведение исследований природы и культурного наследия осуществляется усилиями сотрудников научного отдела, а также учеными из КарНЦ РАН, ПетрГУ, других вузов страны. С некоторыми из них у Парка установились продолжительные и результативные научные и дружественные связи.