Централизованное и рыночное ценообразование. их преимущества и недостатки.

х шт. - вареників зїла Маринка, за умовою задачі.

(х+3) шт. - вареників зїла мама, так як вона зїла на 3 вареники більше ніж Маринка, за умовою задачі.

(х+3)+3 (шт.) - вареників зїв тато, так як він зїв на 3 вареникм більше ніж мама, за умовою задачі.

х+(х+3)+(х+3+3) + вареників зїли Маринка, мама і тато. Це дорівнює

27 шт., за умовою задачі.

Тоді:

х+(х+3)+(х+3+3)=27

х+х+3+х+3+3=27

3х+9=27

3х=27-9

3х=18

х=18 : 3

х=6 (шт.) - вареників зїла Маринка.

6+3=9 (шт.) - вареників зїла мама.

9+3=12 (шт.) - вареників зїв тато.

Перевірка:

6+9+12=27 (шт.) - вареників зїли Маринка, мама і тато, за умовою задачі.

Відповідь: 6 шт.; 9 шт.; 12 шт.

1) Найдем вероятность того, наудачу выбранных 2 человека из 3 человек не отличники.

2) Найдем вероятность того, что среди выбранных 2 человек один отличник.

Количество все возможных исходов: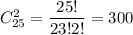

Выбрать одного отличника можно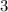 а одного двоечника по правилу произведения таких вариантов 3*22 = 66 - количество благоприятных исходов

Вероятность: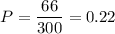

3) Найдем вероятность того, что все выбранные ученики - отличники.

Закон распределения случайной величины X

Математическое ожидание случайной величины X:

Дисперсия случайной величины X: