Дан прямоугольный треугольник ABC, его гипотенуза BC = 2 и tg угла ABC = 2. Найдите наибольшую площадь, которую может иметь прямоугольник, вписанный в этот треугольник так, что одна из его сторон лежит на гипотенузе BC. .
4. Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если:
1) одна на 26 см больше другой, а проекции наклонных равны 12 см и 40 см;
2) наклонные относятся как 1 : 2, а проекции наклонных равны 1 см и 7 см.
1) Проведем SO - перпендикуляр к плоскости α, и обозначим SA = x, SB = y; x > y, так как AO > OB. Из двух прямоугольных тре- угольников SOA и SOB получаем:
2) Обозначим AS = х, тогда AS : SB = 1 : 2, то SB = 2x. SO — перпендикуляр. В прямоугольных треугольниках AOS и BOS имеем:
4. Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если:
1) одна на 26 см больше другой, а проекции наклонных равны 12 см и 40 см;
2) наклонные относятся как 1 : 2, а проекции наклонных равны 1 см и 7 см.
1) Проведем SO - перпендикуляр к плоскости α, и обозначим SA = x, SB = y; x > y, так как AO > OB. Из двух прямоугольных тре- угольников SOA и SOB получаем:
2) Обозначим AS = х, тогда AS : SB = 1 : 2, то SB = 2x. SO — перпендикуляр. В прямоугольных треугольниках AOS и BOS имеем:
Пусть
кг - кислоты в первом растворе в первом сосуде;
тогда
1)
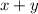кг - кислоты в растворе, полученном путем слияния первых двух растворов из обоих сосудов:
Получаем первое уравнение:
2) 37% = 0,37
Получаем второе уравнение:
3) Решаем систему:
Из первого уравнения выразим
и подставим во второе уравнение:
Во втором растворе 21 кг кислоты
Выразим это в процентном отношении:
ответ: 50%