Мода (при ее наличии) всегда является вариантой ряда. Значит, мода - натуральное число, а тем более целое число.
Размах есть разность между наибольшей и наименьшей вариантой ряда. Значит, размах - разность двух натуральных чисел, то есть целое число.
Медиана ряда, состоящего из нечетного числа вариант, есть варианта, стоящая посередине ряда. Значит, медиана заданного ряда - натуральное число, следовательно и целое число.
Можно привести ряд, среднее арифметическое которого не будет целым числом.
НОД (Наибольший общий делитель) 240 и 264
Наибольший общий делитель (НОД) двух данных чисел 240 и 264 — это наибольшее число, на которое оба числа 240 и 264 делятся без остатка.
НОД (240; 264) = 24.
Как найти наибольший общий делитель для 240 и 264
Разложим на простые множители 240
240 = 2 • 2 • 2 • 2 • 3 • 5
Разложим на простые множители 264
264 = 2 • 2 • 2 • 3 • 11
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 2 , 3
Находим произведение одинаковых простых множителей и записываем ответ
НОД (240; 264) = 2 • 2 • 2 • 3 = 24
НОД (432; 792) = 72.
Как найти наибольший общий делитель для 432 и 792
Разложим на простые множители 432
432 = 2 • 2 • 2 • 2 • 3 • 3 • 3
Разложим на простые множители 792
792 = 2 • 2 • 2 • 3 • 3 • 11
Выберем одинаковые простые множители в обоих числах.
2 , 2 , 2 , 3 , 3
Находим произведение одинаковых простых множителей и записываем ответ
НОД (432; 792) = 2 • 2 • 2 • 3 • 3 = 72
НОД (185; 205) = 5.
Как найти наибольший общий делитель для 185 и 205
Разложим на простые множители 185
185 = 5 • 37
Разложим на простые множители 205
205 = 5 • 41
Выберем одинаковые простые множители в обоих числах.
5
Находим произведение одинаковых простых множителей и записываем ответ
НОД (185; 205) = 5 = 5
Мода (при ее наличии) всегда является вариантой ряда. Значит, мода - натуральное число, а тем более целое число.
Размах есть разность между наибольшей и наименьшей вариантой ряда. Значит, размах - разность двух натуральных чисел, то есть целое число.
Медиана ряда, состоящего из нечетного числа вариант, есть варианта, стоящая посередине ряда. Значит, медиана заданного ряда - натуральное число, следовательно и целое число.
Можно привести ряд, среднее арифметическое которого не будет целым числом.
Пример. Ряд 1, 1, ..., 1, 2.
Среднее арифметическое: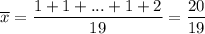
ответ: среднее арифметическое