Дан угол ϕ между диагоналями развёртки боковой поверхности цилиндра, и дана длина диагонали развёртки боковой поверхности b. определи площадь полной поверхности цилиндра.
Из прямоугольника, в котором задана длина диагонали b и угол Ф между диагоналями определим его стороны " alt="S = b*sin\frac{\phi }{2}*b*cos\frac{\phi }{2}+2\pi R^{2} =\frac{1}{2} b^{2} sin\phi +\frac{b^{2}*cos^{2}\frac{\phi}{2} }{2\pi}" />" /> (это высота цилиндра) и (это длина окружности основания цилиндра).
Обозначим радиус окружности основания цилиндра через R, тогда можем записать:
Площадь полной поверхности цилиндра найдем как сумму боковой поверхности и двух оснований:
Из прямоугольника, в котором задана длина диагонали b и угол Ф между диагоналями определим его стороны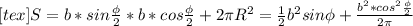 " alt="S = b*sin\frac{\phi }{2}*b*cos\frac{\phi }{2}+2\pi R^{2} =\frac{1}{2} b^{2} sin\phi +\frac{b^{2}*cos^{2}\frac{\phi}{2} }{2\pi}" />" /> (это высота цилиндра) и
" alt="S = b*sin\frac{\phi }{2}*b*cos\frac{\phi }{2}+2\pi R^{2} =\frac{1}{2} b^{2} sin\phi +\frac{b^{2}*cos^{2}\frac{\phi}{2} }{2\pi}" />" /> (это высота цилиндра) и 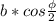 (это длина окружности основания цилиндра).
(это длина окружности основания цилиндра).
Обозначим радиус окружности основания цилиндра через R, тогда можем записать:
Площадь полной поверхности цилиндра найдем как сумму боковой поверхности и двух оснований: