Смотрим в вопрос. Тебя просят найти "сколько времени затратит теплоход на путь..." и бла-бла-бла. Нам нужно найти время. От этого и отталкиваемся.
2) Какими можем ответить на вопрос? Знаем формулу: , из которой нам нужно время. Выразим его для удобства:
3) Смотрим, чего нам не хватает для решения задачи. Первое - это S - расстояние (путь). Мы его знаем? Да, весь путь нам дан - это 120км. Второй пункт - это V - скорость. Вот тут-то всё не так однозначно. Нам дана какая-то скорость и какие-то 75%... Разбираемся.
4) Решение задачи.
В задаче у нас говорится о движущемся теплоходе. Загвоздка в том, что он движется ещё и по реке, у которой есть своя собственная скорость. Как их связать? Если теплоход плывёт по течению, то, логично предположить, что ветер по морю гуляет и кораблик подгоняет) то есть течение реки плыть теплоходу. Поэтому чтобы найти общую скорость передвижения теплохода, нам нужно сложить скорость самого теплохода и скорость реки, по которой он плывёт (если бы теплоход плыл против течения, мы бы от скорости теплохода отнимали течение).
Но вот загвоздка... Мы знаем скорость теплохода (25км/ч), но не знаем скорость течения. Как быть? А вот тут нам пригодится информация о 75%. Сказано, что скорость течения на 75% меньше скорости теплохода. Что делать с этой инфой? Во-первых вспомним, что в данном случае собственная скорость теплохода - это 100%. То есть он плывёт с постоянной скоростью 100%) А вот скорость течения реки на 75% меньше, чем скорость теплохода. Если "на...меньше", то это минус) Стало быть, скорость течения равна 100%-75%=25% от скорости теплохода.
Как найти 25% от скорости теплохода? Во-первых, 25% - это 0.25. Думаю, переводить проценты в десятичную дробь умеем. Чтобы найти какую-то часть от числа, нам нужно это самое число умножить на данную дробь. То есть чтобы найти 25% от 25 км/ч (от скорости теплохода), нам нужно 25*0.25=6.25км/ч. Значит, скорость течения реки равна 6.25км/ч.
Теперь, как ранее было сказано, чтобы найти общую скорость передвижения теплохода, нам нужно сложить скорость самого теплохода и скорость реки. Делаем это.
Мы узнали скорость теплохода. Теперь подставляем в формулу всё, что знаем.
1-й день - 40% = 40/100 = 2/5 всей капусты
2-й день - 60% = 60/100 = 3/5 остатка
3-й день - 96 т
Всего - (целое = 1 или 100%) ?
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
.
1) 100% - 40% = 60% - оставшаяся часть капусты;
2) 60% от 60% = (60·60)/100 = 3600/100 = 36% - отправлено во второй день;
3) 100% - (40% + 36%) = 100% - 76% = 24% - часть капусты, равная 96 т;
4) Находим целое по его части:
96 : 24 · 100 = 4 · 100 = 400 т - столько капусты было на базе.
.
1) 1 - 2/5 = 3/5 - оставшаяся часть капусты;
2) 3/5 · 3/5 = 9/25 - отправлено во второй день;
3) 2/5 + 9/25 = 10/25 + 9/25 = 19/25 - отправлено за два дня;
4) 1 - 19/25 = 6/25 - часть капусты, равная 96 т;
5) Находим целое по его части:
96 : 6/25 = 96 · 25/6 = 16 · 25 = 400 т - столько капусты было на базе.
ответ: 400 т.
Сейчас поймёшь) Смотри.
1) О чём задача?
Смотрим в вопрос. Тебя просят найти "сколько времени затратит теплоход на путь..." и бла-бла-бла. Нам нужно найти время. От этого и отталкиваемся.
2) Какими можем ответить на вопрос? Знаем формулу: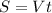
, из которой нам нужно время. Выразим его для удобства: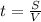 
3) Смотрим, чего нам не хватает для решения задачи. Первое - это S - расстояние (путь). Мы его знаем? Да, весь путь нам дан - это 120км. Второй пункт - это V - скорость. Вот тут-то всё не так однозначно. Нам дана какая-то скорость и какие-то 75%... Разбираемся.
4) Решение задачи.
В задаче у нас говорится о движущемся теплоходе. Загвоздка в том, что он движется ещё и по реке, у которой есть своя собственная скорость. Как их связать? Если теплоход плывёт по течению, то, логично предположить, что ветер по морю гуляет и кораблик подгоняет) то есть течение реки плыть теплоходу. Поэтому чтобы найти общую скорость передвижения теплохода, нам нужно сложить скорость самого теплохода и скорость реки, по которой он плывёт (если бы теплоход плыл против течения, мы бы от скорости теплохода отнимали течение).
Но вот загвоздка... Мы знаем скорость теплохода (25км/ч), но не знаем скорость течения. Как быть? А вот тут нам пригодится информация о 75%. Сказано, что скорость течения на 75% меньше скорости теплохода. Что делать с этой инфой? Во-первых вспомним, что в данном случае собственная скорость теплохода - это 100%. То есть он плывёт с постоянной скоростью 100%) А вот скорость течения реки на 75% меньше, чем скорость теплохода. Если "на...меньше", то это минус) Стало быть, скорость течения равна 100%-75%=25% от скорости теплохода.
Как найти 25% от скорости теплохода? Во-первых, 25% - это 0.25. Думаю, переводить проценты в десятичную дробь умеем. Чтобы найти какую-то часть от числа, нам нужно это самое число умножить на данную дробь. То есть чтобы найти 25% от 25 км/ч (от скорости теплохода), нам нужно 25*0.25=6.25км/ч. Значит, скорость течения реки равна 6.25км/ч.
Теперь, как ранее было сказано, чтобы найти общую скорость передвижения теплохода, нам нужно сложить скорость самого теплохода и скорость реки. Делаем это.
Мы узнали скорость теплохода. Теперь подставляем в формулу всё, что знаем.
ответ: 3,84 часа.