Пошаговое объяснение:
Так как в данной задаче сумма каждого столбца
должна быть равна 1, ⇒
Матрица приобретает вид:
Найдём собственный вектор х'', отвечающий
собственному значению λ=1.
Для этого решим уравнение: (А-Е)*х''=0''.
Найдём А-Е:
Тогда еравнение (А-Е)*х''=0'' можно записать в виде следующей однородной системы линейных алгебраических
уравнений:
Выполним преобразования.
Умножим первое уравнение на -6, второе уравнение на 3,
а третье уравненик на 12:
Решим эту систему методом Гаусса.
Запишем расширенную матрицу системы:
Разделим вторую строку на 2:
Поменяем местами первую и вторую строки:
Прибавим ко второй строке первую, умноженную на -3:
Прибавим к третьей строке первую, умноженную на -2:
Прибавим к третьей строке вторую, умноженную на 4:
Таким образом:
Разделим третью строку на -30:
Следовательно:
Пусть х₃=с ⇒
ответ: x₁:x₂:x₃=12:10:3.
1. Метод исключения неизвестных.
Продифференцируем первое уравнение:
Подставим выражение для y':
Из получившегося уравнения отнимем первое уравнение системы:
Составим характеристическое уравнение:
Найдем производную:
Выразим из первого уравнение системы у:
Общее решение:
Находим решение задачи Коши:
Первое уравнение домножим на 2:
Сложим уравнения:
Выразим :
Частное решение:
2. Метод характеристических уравнений (метод Эйлера).
Матрица из коэффициентов при неизвестных:
Характеристическая матрица:
Характеристическое уравнение:
Ищем фундаментальную систему решений:
Для нахождения чисел составим систему:
Для :
Оба уравнения дают:
Найдем ненулевое решение. Пусть . Тогда .
Фундаментальная система решений найдена:
Находим частное решение:
Пошаговое объяснение:
Так как в данной задаче сумма каждого столбца
должна быть равна 1, ⇒
Матрица приобретает вид:
Найдём собственный вектор х'', отвечающий
собственному значению λ=1.
Для этого решим уравнение: (А-Е)*х''=0''.
Найдём А-Е:
Тогда еравнение (А-Е)*х''=0'' можно записать в виде следующей однородной системы линейных алгебраических
уравнений:
Выполним преобразования.
Умножим первое уравнение на -6, второе уравнение на 3,
а третье уравненик на 12:
Решим эту систему методом Гаусса.
Запишем расширенную матрицу системы:
Разделим вторую строку на 2:
Поменяем местами первую и вторую строки:
Прибавим ко второй строке первую, умноженную на -3:
Прибавим к третьей строке первую, умноженную на -2:
Прибавим к третьей строке вторую, умноженную на 4:
Таким образом:
Разделим третью строку на -30:
Следовательно:
Пусть х₃=с ⇒
ответ: x₁:x₂:x₃=12:10:3.
1. Метод исключения неизвестных.
Продифференцируем первое уравнение:
Подставим выражение для y':
Из получившегося уравнения отнимем первое уравнение системы:
Составим характеристическое уравнение:
Найдем производную:
Выразим из первого уравнение системы у:
Общее решение:
Находим решение задачи Коши:
Первое уравнение домножим на 2:
Сложим уравнения:
Выразим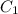 :
:
Частное решение:
2. Метод характеристических уравнений (метод Эйлера).
Матрица из коэффициентов при неизвестных:
Характеристическая матрица:
Характеристическое уравнение:
Общее решение:
Ищем фундаментальную систему решений:
Для нахождения чисел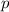 составим систему:
составим систему:
Для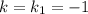 :
:
Оба уравнения дают:
Найдем ненулевое решение. Пусть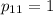 . Тогда
. Тогда 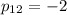 .
.
Для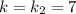 :
:
Оба уравнения дают:
Найдем ненулевое решение. Пусть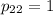 . Тогда
. Тогда 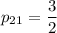 .
.
Фундаментальная система решений найдена:
Общее решение:
Находим частное решение:
Первое уравнение домножим на 2:
Сложим уравнения:
Выразим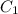 :
:
Частное решение: