Для покриття підлоги будуть використовувати плитку, що має форму
рівнобічної трапеції, основи якої дорівнюють 20 см і 40 см, а кут при
більшій основі дорівнює 45. запропонуйте свої варіанти покриття підлоги
даною плиткою для кімнати, підлога якої є прямокутником розміром
6 10 м (деякі плитки можна розрізати на частини). іть будь ласка
Откроешь кран и подставив ладонь под струю отрегулируешь её так что бы она попала на шторы и потушишь их если ты спокойный ( ещё их сорвать желательно как нибудь ), ну или пойдёшь и возьмёшь огнетушитель если такой имеется на даче, если ты спокойный.
И вообще ответный вопрос: А как ты проморгал то что работает плита и какова вероятность то что штора лежала так долго на плите что загорелась(ветер же мог её и обратно сдуть или просто с плиты сдуть)
Раз некоторое число удовлетворяет уравнению при любом
удовлетворяет уравнению при любом  , то оно также удовлетворяет уравнению при
, то оно также удовлетворяет уравнению при 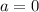 .
.
То есть, если мы подставим в уравнение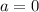 , то выполнится равенство:
, то выполнится равенство:
Оба корня удовлетворяют уравнению и ОДЗ (при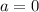 ): с обеих сторон в первом случае получается
): с обеих сторон в первом случае получается  , а во втором
, а во втором 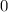 (так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
(так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
Очевидно, что эти два корня в ответ так сразу не пойдут. Мы знаем лишь только, что они подходят при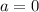 . И если ответ на задачу существует, то он может быть только
. И если ответ на задачу существует, то он может быть только 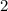 ,
, 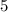 или и
или и 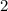 , и
, и 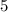 . Но про другие значения
. Но про другие значения  мы пока ничего не знаем.
мы пока ничего не знаем.
Посмотрим, что у нас будет получаться при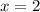 :
:
Вот только первый логарифм не всегда существует.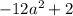 может быть отрицательным (возьмите, к примеру,
может быть отрицательным (возьмите, к примеру, 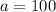 ). А подлогарифмическое выражение обязано быть положительным. Значит, такой
). А подлогарифмическое выражение обязано быть положительным. Значит, такой  нас не устраивает.
нас не устраивает.
Теперь проверим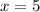 :
:
В обеих частях мы получили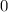 (так как
(так как 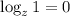 , если
, если 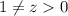 ). Также
). Также 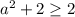 , поэтому все ограничения будут выполняться.
, поэтому все ограничения будут выполняться.
В итоге имеем нужный ответ: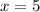 .
.
Задача решена!