Разобьём данную систему из трёх уравнений на две системы из двух уравнений:
В первой системе складываем верхнее и нижнее уравнения. Получается вот так:
Мы избавились от переменной и получили новое уравнение с двумя переменными. Теперь во второй системе нам тоже нужно избавиться от неё. Чтобы это сделать, умножим верхнее уравнение на 8:
И тоже складываем их между собой:
Теперь мы имеем 2 уравнения с 2 переменными. Составляем из них новую систему и решаем её.
Умножим верхнее уравнение на -6:
И складываем их между собой:
Нашли значение , теперь подставим его в любое уравнение системы с 2 уравнениями, пускай в верхнее:
И теперь подставим эти 2 значения в любое из уравнений изначальной системы, пусть во второе:
Получили три значения, по которым можно восстановить первоначальный вид функции: . Теперь можно проверить каждое из условий, чтобы убедиться в правильности найденных значений.
ответ: верный последний ответ. ложное утверждение Число 7 является корнем уравнения |2021 у - 2022| = 8049
Пошаговое объяснение:
первое не имеет корней. т.к. модуль число неотрицательное, т.к. выражает расстояние. истинное.
2. Число (-9) является корнем уравнения |-х- 1 - 1 - 1 | = 6, т.к. Число (-9) является корнем уравнения |-(-9)- 1 - 1 - 1 | = 6, |9- 1 - 1 - 1 | = 6, 6=6- истинное.
3. |-5*z- 8 |+3 = 10 имеет более одного решения истинное, т.к. |-5*z- 8 |=7
если -5*z- 8 =7 , то 5z=-15; z=-3; а если -5*z- 8 =-7, то 5z=-1, z=-1/5, два корня, т.е. более одного.
4. подставим. проверим. получим |2021*7 - 2022| ≠ 8049, т.к.
|2021*7 - 2022|= |14147 - 2022|= |12125|=12125≠8049
Составляем систему уравнений:
Раскрываем скобки, получаем вот такую систему:
Разобьём данную систему из трёх уравнений на две системы из двух уравнений:
В первой системе складываем верхнее и нижнее уравнения. Получается вот так:
Мы избавились от переменной и получили новое уравнение с двумя переменными. Теперь во второй системе нам тоже нужно избавиться от неё. Чтобы это сделать, умножим верхнее уравнение на 8:
и получили новое уравнение с двумя переменными. Теперь во второй системе нам тоже нужно избавиться от неё. Чтобы это сделать, умножим верхнее уравнение на 8:
И тоже складываем их между собой:
Теперь мы имеем 2 уравнения с 2 переменными. Составляем из них новую систему и решаем её.
Умножим верхнее уравнение на -6:
И складываем их между собой:
Нашли значение , теперь подставим его в любое уравнение системы с 2 уравнениями, пускай в верхнее:
, теперь подставим его в любое уравнение системы с 2 уравнениями, пускай в верхнее:
И теперь подставим эти 2 значения в любое из уравнений изначальной системы, пусть во второе:
Получили три значения, по которым можно восстановить первоначальный вид функции: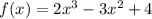 . Теперь можно проверить каждое из условий, чтобы убедиться в правильности найденных значений.
. Теперь можно проверить каждое из условий, чтобы убедиться в правильности найденных значений.
ответ: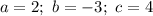 .
.