Доказать, что если числа а, a+d, a+2d,..., a+(n–1)d - вопрос №2120743063 от kodraemail 13.04.2021 18:53

Question

Математика: Доказать, что если числа а, a+d, a+2d,..., a+(n–1)d целые и взаимно простые числа с n, то d и n не взаимно простые.

kodraemail · Answer

Пусть не так, и и числа n и d взаимно простые.

Покажем, что никакие 2 числа из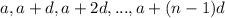 a, a+d, a+2d,..., a+(n-1)d не могут давать одинаковые остатки от деления на n.

Пусть не так, и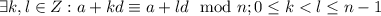 $\exists k,l\in Z:a+kd\equiv a+ld \mod n; 0\leq k$ .

Но тогда их разность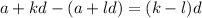 a+kd-(a+ld)=(k-l)d делится на n. Отсюда следует, с учетом взаимной простоты n и d, что 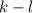k-l делится на n. Но, нетрудно заметить, 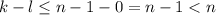$k-l\leq n-1-0=n-1$ - противоречие.

Значит, числа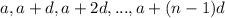 a, a+d, a+2d,..., a+(n-1)d дают различные остатки при делении на n. Но этих чисел ровно n - значит, среди них обязательно найдется число, дающее остаток 0 при делении на n. Противоречие с тем, что числа 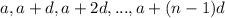a, a+d, a+2d,..., a+(n-1)d взаимно простые с n.

Это и означает, что числа n и d не взаимно простые.

Ч.т.д.