Докажите, что среди чисел вида 2^{n} -3 существует бесконечно много чисел, делящихся на 5, и бесконечно много чисел, делящихся на 13, но не существует ни одного числа, делящегося на 65. Указание: рассмотреть остатки от деления числа на 5 и 13

Показать ответ

Ответ:

AkiraK666

15.10.2020 15:26

Разность чисел a и b делится на c, если a и b имеют равные остатки при делении на с.

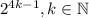Рассмотрим остатки от деления данного выражения на 5. 3 имеет остаток 3, поэтому 2ⁿ также должно иметь остаток 3. Заметим, что все числа вида $2^{4k-1},k\in\mathbb{N}$ имеют такой остаток. Докажем это методом математической индукции:

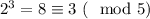
1. База индукции: при k = 1 $2^3=8\equiv 3\ (\mod 5)$

2. Переход: пусть при k = x утверждение верно. Тогда при k = x + 1:

$2^{4(x+1)-1}=2^{4x+3}=16\cdot2^{4x-1}\equiv 1\cdot2^{4x-1}\ (\mod 5)$

Утверждение доказано. Так как k — любое натуральное число, данных в условии чисел бесконечно много.

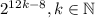Аналогично 2ⁿ должно иметь остаток 3 при делении на 13. Также докажем по индукции, что числа вида $2^{12k-8},k\in\mathbb{N}$ подходят:

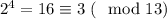
1. База индукции: при k = 1 $2^4=16\equiv 3\ (\mod 13)$

2. Переход: пусть при k = x утверждение верно. Тогда при k = x + 1:

$2^{12(x+1)-8}=2^{12x+4}=2^{12}\cdot2^{12x-8}\equiv 1\cdot2^{12x-8}\ (\mod 13)$

Утверждение доказано, данных в условии чисел, делящихся на 13, бесконечно много.

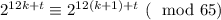Докажем, что не существует чисел вида 2ⁿ, которые при делении на 65 дают остаток 3. Выпишем первые 12 остатков: 2 4 8 16 32 64 63 61 57 49 33 1. Среди них нет ни одной тройки. Докажем, что они повторяются, то есть $2^{12k+t}\equiv 2^{12(k+1)+t}\ (\mod 65)$ , где k — неотрицательное целое число, 0 ≤ t ≤ 11 (за исключением случая k = t = 0):