Х- время до встречи 1- весь путь 1/(х+25)- скорость первого 1/(х+36)-скорость второго
Совместная скорость 1/(х+25)+1/(х+36)
х(1/(х+25)+1/(х+36))=1 х/(х+25)+х/(х+36)=1 Домножим на (х+25)(х+36) х(х+36)+х(х+25)=(х+25)(х+36) х^2+36x+x^2+25x=x^2+36x+25x+900 х^2+х^2-х^2+36x+25x-36x-25x=900 х^2=900 x=-30 не подходит х=30мин=0,5ч
2.Пусть число это хукм 1000х+100у+10к+м+х+у+к+м=2014 1001х+101у+11к+2м=2014 х>2 быть не может, т.к. 1001*3=3003 больше 2014 значит рассматриваем четырехзначные числа в диапазоне от 1000 до 2999
рассмотрим диапазон 2000-2999 (т.е.х=2) 1001х=2002, значит 101у+11к+2м=2014-2002=12, следовательно у>0 не подходит, т.к. 101*1=101. Т.О. у=0. Получается 11к+2м=12, следовательно к>1 не подходит, т.к. 11*2=22, получается 11*1+2м=12 11+2м=12 2м=1 м=0,5 - не подходит, т.к. должно быть целое число, т.о. к=0 Получается 2м=12 м=6 Единственное число из диапазона 2000-2999 это 2006.
рассмотрим диапазон 1000-1999 (т.е. х=1)
1001х+101у+11к+2м=2014 1001*1=1001 101у+11к+2м=2014-1001 101у+11к+2м=1013 при у<9 в максимуме 899 получается 101*8+11*9+2*9=808+99+18=925, что меньше 1013, значит у=9. Следовательно, 101*9+11к+2м=1013 11к+2м=1013-909=104 При к<8 в максимуме 79 получается 11*7+2*9=77+18=95, что меньше 104, значит подходят к=8 и к=9
рассмотрим к=8 11*8+2м=104 88+2м=104 2м=104-88=16 м=8 Т.о. первое число из диапазона 1000-1999 это 1988
рассмотрим к=9 11*9+2м=104 99+2м=104 2м=104-99=5 м=2,5- не подходит, т.к. должно быть целое число.
1- весь путь
1/(х+25)- скорость первого
1/(х+36)-скорость второго
Совместная скорость 1/(х+25)+1/(х+36)
х(1/(х+25)+1/(х+36))=1
х/(х+25)+х/(х+36)=1 Домножим на (х+25)(х+36)
х(х+36)+х(х+25)=(х+25)(х+36)
х^2+36x+x^2+25x=x^2+36x+25x+900
х^2+х^2-х^2+36x+25x-36x-25x=900
х^2=900
x=-30 не подходит
х=30мин=0,5ч
2.Пусть число это хукм
1000х+100у+10к+м+х+у+к+м=2014
1001х+101у+11к+2м=2014
х>2 быть не может, т.к. 1001*3=3003 больше 2014
значит рассматриваем четырехзначные числа в диапазоне от 1000 до 2999
рассмотрим диапазон 2000-2999 (т.е.х=2)
1001х=2002, значит 101у+11к+2м=2014-2002=12, следовательно у>0 не подходит, т.к.
101*1=101. Т.О. у=0.
Получается 11к+2м=12, следовательно к>1 не подходит, т.к. 11*2=22,
получается
11*1+2м=12
11+2м=12
2м=1
м=0,5 - не подходит, т.к. должно быть целое число, т.о. к=0
Получается 2м=12
м=6
Единственное число из диапазона 2000-2999 это 2006.
рассмотрим диапазон 1000-1999 (т.е. х=1)
1001х+101у+11к+2м=2014
1001*1=1001
101у+11к+2м=2014-1001
101у+11к+2м=1013
при у<9 в максимуме 899 получается 101*8+11*9+2*9=808+99+18=925, что меньше 1013,
значит у=9.
Следовательно,
101*9+11к+2м=1013
11к+2м=1013-909=104
При к<8 в максимуме 79 получается 11*7+2*9=77+18=95, что меньше 104,
значит подходят к=8 и к=9
рассмотрим к=8
11*8+2м=104
88+2м=104
2м=104-88=16
м=8
Т.о. первое число из диапазона 1000-1999 это 1988
рассмотрим к=9
11*9+2м=104
99+2м=104
2м=104-99=5
м=2,5- не подходит, т.к. должно быть целое число.
ответ: два числа 2006 и 1988
Дан полушар с радиусом R = OC и описанный около него конус с радиусом основания r = OA и высотой h = OM.
Построим сечение конуса по диаметру основания : ΔAMB
OM - высота конуса ⇒ ΔAMO - прямоугольный. Пусть ∠OMK=α
OK⊥AM - как радиус шара в точку касания с конусом ⇒ ΔOKM - прямоугольный. По отношению сторон прямоугольного треугольника :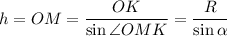
По отношению сторон прямоугольного треугольника ΔAMO:
Тогда объём конуса по формуле
Объём конуса, выраженный дробью, будет наименьшим, когда знаменатель будет наибольшим.
Наибольшее значение функции в знаменателе можно найти через производную.
f (α) = sin α - sin³ α
f'(α) = (sin α - sin³ α)' = 0
cos α - 3 sin² α cos α = 0
cos α (1 - 3 sin²α) = 0
1) cos α = 0 ⇒ α = 90° - не подходит по условию (угол при вершине сечения не может быть равен 180°).
1 - 3 sin²α = 0 ⇒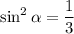 ⇒
⇒
Высота конуса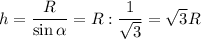
ответ: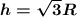
=======================================
Наименьший объём описанного конуса с высотой h=√3 R