Две феи купили 9 одинаковых волшебных палочек и поспорили о том кто из них должен взять себе больше волшебных палочек феям справедливо разделить волшебные палочки если первая фея потратила 210 волшебных монет а вторая 420 такие же монет?
Мода (при ее наличии) всегда является вариантой ряда. Значит, мода - натуральное число, а тем более целое число.
Размах есть разность между наибольшей и наименьшей вариантой ряда. Значит, размах - разность двух натуральных чисел, то есть целое число.
Медиана ряда, состоящего из нечетного числа вариант, есть варианта, стоящая посередине ряда. Значит, медиана заданного ряда - натуральное число, следовательно и целое число.
Можно привести ряд, среднее арифметическое которого не будет целым числом.
Мода (при ее наличии) всегда является вариантой ряда. Значит, мода - натуральное число, а тем более целое число.
Размах есть разность между наибольшей и наименьшей вариантой ряда. Значит, размах - разность двух натуральных чисел, то есть целое число.
Медиана ряда, состоящего из нечетного числа вариант, есть варианта, стоящая посередине ряда. Значит, медиана заданного ряда - натуральное число, следовательно и целое число.
Можно привести ряд, среднее арифметическое которого не будет целым числом.
Мода (при ее наличии) всегда является вариантой ряда. Значит, мода - натуральное число, а тем более целое число.
Размах есть разность между наибольшей и наименьшей вариантой ряда. Значит, размах - разность двух натуральных чисел, то есть целое число.
Медиана ряда, состоящего из нечетного числа вариант, есть варианта, стоящая посередине ряда. Значит, медиана заданного ряда - натуральное число, следовательно и целое число.
Можно привести ряд, среднее арифметическое которого не будет целым числом.
Пример. Ряд 1, 1, ..., 1, 2.
Среднее арифметическое: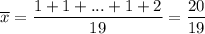
ответ: среднее арифметическое
Мода (при ее наличии) всегда является вариантой ряда. Значит, мода - натуральное число, а тем более целое число.
Размах есть разность между наибольшей и наименьшей вариантой ряда. Значит, размах - разность двух натуральных чисел, то есть целое число.
Медиана ряда, состоящего из нечетного числа вариант, есть варианта, стоящая посередине ряда. Значит, медиана заданного ряда - натуральное число, следовательно и целое число.
Можно привести ряд, среднее арифметическое которого не будет целым числом.
Пример. Ряд 1, 1, ..., 1, 2.
Среднее арифметическое: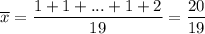
ответ: среднее арифметическое