Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
Пусть , тогда .
Делаем подстановку в наше изначальное выражение:
Здесь сокращаются и мы имеем . Выносим за интеграл: . Теперь мы имеем знакомый интеграл, который равняется , тоже самое что . Подставляем и имеем . Используем фундаментальную теорему исчисления:
ответ: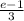
Пошаговое объяснение:
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
Пусть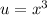
, тогда ![x=\sqrt[3]{u}](/tpl/images/1117/3966/8c879.png)
.
Делаем подстановку в наше изначальное выражение:
Здесь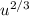
сокращаются и мы имеем 
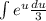. Выносим 
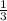за интеграл: 
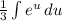. Теперь мы имеем знакомый интеграл, который равняется 
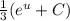, тоже самое что 
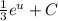. Подставляем 
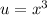и имеем 
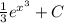. Используем фундаментальную теорему исчисления:
Пошаговое объяснение:
1) б)
6х – 2 = 2х + 6
6x - 2x = 6 + 2
4x = 8
x = 8 : 4
x = 2
в)
11 + 7х = 55 + 3х
7x - 3x = 55 - 11
4x = 44
x = 44 : 4
x = 11
г)
− 8х + 17 = 3х + 83
3x + 8x = 17 - 83
11x = -66
x = -66 : 11
x = -6
2)а)
5(2 + у) = 4 – 3у
10 + 5y = 4 - 3y
5y + 3y = 4 - 10
8y = -6
y = -6 : 8
y = -0,75
б)
−2(3b + 1) – 14 = 8
-6b - 2 - 14 = 8
-6b - 16 = 8
6b = -16 - 8
6b = -24
b = -24 : 6
b = -4
в)
−3(2 – 5х) = 6(х + 3) – 6
-6 + 15x = 6x + 18 - 6
-6 + 15x = 6x + 12
15x - 6x = 12 + 6
9x = 18
x = 18 : 9
x = 2
г)
– 3,92у – (1,08у + 5,07) = − 0,89 – у
-3,92y - 1,08y - 5,07 = -0,89 - y
-5y - 5,07 = -0,89 - y
5y - y = -5,07 + 0,89
4y = -4,18
y = -4,18 : 4
y = -1,045