Математика: Ф. Бер: АБСБ - micмop miqрли, Б (38) С(п: -Ч) УСІ; -6) П/k: (x; ) =?

Ф. Бер: АБСБ - micмop miqрли,
Б (38)
С(п: -Ч)
УСІ; -6)
П/k: (x; ) =?

Показать ответ

Ответ:

nlenp6635Alena0lo

20.07.2020 14:02

Пошаговое объяснение:

в)

критические точки (точки смены знаков)

f'(x) = 4x-1

4x-1 = 0 ⇒ х =0,25

получили два интервала и посмотрим знаки производной на каждом из них

(-∞; 0,25) f'(0)=-1 < 0 функция убывает

(0,25; +∞) f'(1)=3 > 0 функция возрастает

(на графике красная линия)

г)

здесь х = 0 - точка разрыва.

посмотрим, есть ли еще какие подозрительные точки

f'(x_ = -1/x² нулей нет, есть всё та же точка разрыва х=0

значит интервалы смотрим и знаки производных на этих интервалах

(-∞; 0) f'(-1) = -1 < 0 функция убывает

(0; +∞) f'(1) = -1 < 0 функция убывает

на графике две синих линии

х = 0 - зеленая линия

Найдите промежутки возрастания и убывания функции f (x). в)f(x)=2x^2-x. г)f(x)=1/x+1

0,0(0 оценок)

Ответ:

Камишок7

22.02.2023 00:01

Відповідь:

Покрокове пояснення:

Немного не то, смотрите: когда у нас просят вычислить площадь фигуры (или же трапеции), ограниченной линиями, тогда мы должны использовать формулу Ньютона-Лейбница: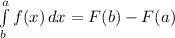 $\int\limits^a_b {f(x)} \, dx =F(b)-F(a)$ - простыми словами, находим интегралы линии, которой ограничена трапеция, a и b - на каком отрезке расположена трапеция.

Сперва в задаче нужно нарисовать графики и прямые на числовой прямой, что указаны в условии: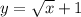 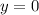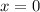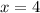$y=\sqrt{x} +1$ , y=0 , x=0 , x=4 . Примерный график прикрепляю.

Глядя на рисунок, можем сказать, что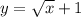 $y=\sqrt{x}+1$ расположен над осью ОХ, значит можем найти площадь таким образом: 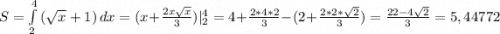$S=\int\limits^4_2 {(\sqrt{x}+1)} \, dx =(x+\frac{2x\sqrt{x}}{3})|^4_2=4+\frac{2*4*2}{3}-(2+\frac{2*2*\sqrt{2}}{3})=\frac{22-4\sqrt{2}}{3}=5,44772$ см²