Используя формулы преобразования суммы и разности тригонометрических функций в произведение , упростите выражение cos 3a-cos5a и найдите его значение, если cosa=1/√3

Показать ответ

Ответ:

mimimi055

15.04.2021 08:27

Распилить третье звено. Получится три части цепочки: одна часть будет состоять из двух звеньев, вторая - из четырёх, третья часть - одно распиленное звено.

1-й день - путешественник отдаёт распиленное звено;

2-й день - даёт часть из 2 звеньев, распиленное звено получает обратно;

3-й день - путешественник отдаёт распиленное звено;

4-й день - даёт часть из 4 звеньев, распиленное звено и часть из 2 звеньев получает обратно;

5-й день - путешественник отдаёт распиленное звено;

6-й день - даёт часть из 2 звеньев, распиленное звено получает обратно;

7-й день - путешественник отдаёт распиленное звено.

0,0(0 оценок)

Ответ:

илья20032101

18.02.2020 16:06

1 ч. 5 мин.=13/12 ч.

Пусть х км/ч - скорость на подъёме, тогда скорость на спуске - (х+2) км/ч. Пусть у км - расстояние от станции до вершины горы, тогда расстояние от вершины горы до озера - (5-у) км. На дорогу от станции до озера рыболов затратил у/х + (5-у)/(х+2) или 1 час; на обратную дорогу - (5-у)/х + у/(х+2) или 13/12 часа. Составим и решим систему уравнений:

$\left \{ {{\frac{y}{x}+\frac{5-y}{x+2}=1} \atop {\frac{5-y}{x}+\frac{y}{x+2}=\frac{13}{12}}} \right$

$\left \{ {{xy+2y+5x-xy=x(x+2)} \atop {5x-xy+10-2y+xy=\frac{13x(x+2)}{12}}} \right$

$\left \{ {{2y=x^2+2x-5x} \atop {-2y=\frac{13x^2}{12}+\frac{13x}{6}-5x-10}} \right$

$\left \{ {{2y=x^2-3x} \atop {-2y=\frac{13x^2}{12}-\frac{17x}{6}-10}} \right$

Произведём подстановку:

$\left \{ {{2y=x^2-3x} \atop {-x^2+3x=\frac{13x^2}{12}-\frac{17x}{6}-10}} \right$

$\left \{ {{2y=x^2-3x} \atop {\frac{13x^2}{12}-\frac{17x}{6}-10+x^2-3x=0}} \right$

$\left \{ {{2y=x^2-3x} \atop {\frac{25x^2}{12}-\frac{35x}{6}-10=0}} \right$

Домножим второе уравнение на 12/25:

$\left \{ {{2y=x^2-3x} \atop {x^2-2,8x-4,8=0}} \right$

По теореме Виета корнями уравнения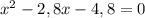 $x^{2}-2,8x-4,8=0$ являются 4 и -1,2. Так как скорость не может быть отрицательным числом, получаем, что скорость на подъёме была равна 4 км/ч, а на спуске 4+2=6 км/ч.