Для 1-ого случая можно использовать 1-ый чертеж с введенными в объяснении уточнениями, исключив ненужные построения.
Заметим, что треугольник AOB прямоугольный и равнобедренный. Тогда его высота (назовем ее OH) совпадает с медианой и равна . По теореме о трех перпендикулярах MH будет высотой треугольника ABM, а так как OM перпендикулярна плоскости квадрата ABCD, то по теореме Пифагора . Откуда см².
Приведу другое решение задачи:
Проведем AO. Поскольку OM перпендикулярен плоскости, то ΔAOM прямоугольный. Заметим, что AO - половина диагонали квадрата, так как точка O - центр квадрата.
Найдем AO:
По теореме Пифагора для ΔAOM:
Аналогично , так как диагонали квадрата равны.
Искать площадь по формуле Герона не удобно, так как получили значения с корнями.
Поэтому воспользуемся теоремой косинусов:
Тогда площадь треугольника ABM равна:
Получили, что площадь треугольника ABM равна 135см².
Замечу, что в задаче не указано, что центр квадрата - это точка O. Так принято. Однако возможен другой случай, где эти точки поменяны местами. Тогда . Единицы измерения см².
Чтобы решить эту задачу, нам понадобятся основные свойства прямоугольных треугольников, квадратов и перпендикуляров.
Во-первых, давайте посмотрим на основные свойства прямоугольных треугольников. В них один из углов равен 90 градусов. В нашей задаче перпендикуляр ОМ восстановлен к плоскости квадрата АВСD, поэтому треугольник АМО является прямоугольным.
Зная, что ОМ равен 12 см, и у нас есть прямоугольный треугольник, мы можем использовать теорему Пифагора, чтобы найти длину гипотенузы АМ треугольника АМО.
По теореме Пифагора:
гипотенуза² = катет₁² + катет₂².
Так как М — это середина стороны AB, то катет1 равен половине стороны АВ, то есть 18 см / 2 = 9 см.
Исходя из того, что ОМ равен 12 см, мы можем найти длину гипотенузы АМ:
гипотенуза² = 9² + 12² = 81 + 144 = 225.
Возведем гипотенузу в квадрат: √225 = 15 см.
Теперь, когда у нас есть длина гипотенузы АМ, мы можем найти площадь треугольника АМВ по формуле:
площадь = 0,5 * основание * высота.
Основанием треугольника АМВ будет сторона АВ квадрата, то есть 18 см.
Высотой треугольника АМВ будет перпендикуляр ОМ, который равен 12 см.
Подставим значения в формулу:
площадь = 0,5 * 18 см * 12 см = 108 см².
Итак, площадь треугольника АВМ составляет 108 квадратных сантиметров.
(см. объяснение)
Пошаговое объяснение:
Чертежи приведены ко 2-ому и 3-ему случаям!
Для 1-ого случая можно использовать 1-ый чертеж с введенными в объяснении уточнениями, исключив ненужные построения.
Заметим, что треугольник AOB прямоугольный и равнобедренный. Тогда его высота (назовем ее OH) совпадает с медианой и равна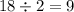 . По теореме о трех перпендикулярах MH будет высотой треугольника ABM, а так как OM перпендикулярна плоскости квадрата ABCD, то по теореме Пифагора
. По теореме о трех перпендикулярах MH будет высотой треугольника ABM, а так как OM перпендикулярна плоскости квадрата ABCD, то по теореме Пифагора 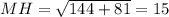 . Откуда
. Откуда 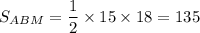 см².
см².
Приведу другое решение задачи:
Проведем AO. Поскольку OM перпендикулярен плоскости, то ΔAOM прямоугольный. Заметим, что AO - половина диагонали квадрата, так как точка O - центр квадрата.
Найдем AO:
По теореме Пифагора для ΔAOM:
Аналогично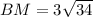 , так как диагонали квадрата равны.
, так как диагонали квадрата равны.
Искать площадь по формуле Герона не удобно, так как получили значения с корнями.
Поэтому воспользуемся теоремой косинусов:
Тогда площадь треугольника ABM равна:
Получили, что площадь треугольника ABM равна 135см².
Замечу, что в задаче не указано, что центр квадрата - это точка O. Так принято. Однако возможен другой случай, где эти точки поменяны местами. Тогда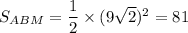 . Единицы измерения см².
. Единицы измерения см².
Во-первых, давайте посмотрим на основные свойства прямоугольных треугольников. В них один из углов равен 90 градусов. В нашей задаче перпендикуляр ОМ восстановлен к плоскости квадрата АВСD, поэтому треугольник АМО является прямоугольным.
Зная, что ОМ равен 12 см, и у нас есть прямоугольный треугольник, мы можем использовать теорему Пифагора, чтобы найти длину гипотенузы АМ треугольника АМО.
По теореме Пифагора:
гипотенуза² = катет₁² + катет₂².
Так как М — это середина стороны AB, то катет1 равен половине стороны АВ, то есть 18 см / 2 = 9 см.
Исходя из того, что ОМ равен 12 см, мы можем найти длину гипотенузы АМ:
гипотенуза² = 9² + 12² = 81 + 144 = 225.
Возведем гипотенузу в квадрат: √225 = 15 см.
Теперь, когда у нас есть длина гипотенузы АМ, мы можем найти площадь треугольника АМВ по формуле:
площадь = 0,5 * основание * высота.
Основанием треугольника АМВ будет сторона АВ квадрата, то есть 18 см.
Высотой треугольника АМВ будет перпендикуляр ОМ, который равен 12 см.
Подставим значения в формулу:
площадь = 0,5 * 18 см * 12 см = 108 см².
Итак, площадь треугольника АВМ составляет 108 квадратных сантиметров.