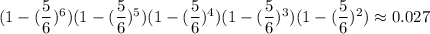Известно, что средние издержки на выпуск 49-й единицы продукции равны 8, а предельные издержки на выпуск 50-й единицы равны 28. Чему будут равны средние издержки на выпуск 50-й единицы продукции?

8 км.

Пошаговое объяснение:

Обозначим длину участка в гору а, ровного b, под гору с. Нам нужно найти b.

Когда пешеход идёт обратно из D в А, то длина в гору с, а длина под гору а.

Время пути от А до D:

a/3 + b/4 + c/5 = 5 ч 48 мин = 348/60 ч

Время пути от D до А:

a/5 + b/4 + c/3 = 6 ч 12 мин = 372/60 ч

Дорога имеет длину 23 км

a + b + c = 23

Умножаем все на 3*4*5 = 60

{ 20a + 15b + 12c = 348

{ 12a + 15b + 20c = 372

{ a + b + c = 23

Вычитаем из 2 уравнения 1 уравнение

-8a + 8c = 24

c - a = 3; c = a + 3

Подставляем в уравнения

{ 20a + 15b + 12(a + 3) = 348

{ a + b + a + 3 = 23

Раскрываем скобки

{ 20a + 15b + 12a + 36 = 348

{ 2a + b = 20

Приводим подобные

{ 32a + 15b = 312

{ b = 20 - 2a

Подставляем b в 1 уравнение

32a + 15(20 - 2a) = 312

32a + 300 - 30a = 312

2a = 12

a = 6 км; b = 20 - 2a = 20 - 12 = 8 км; c = a + 3 = 6 + 3 = 9 км.

Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков

Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда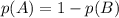

Вероятность не угадать число на одном кубике равна (среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна 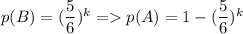  - это и есть искомая вероятность в данной задаче.

Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна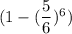 . При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна 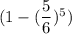. При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна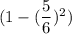

Тогда искомая вероятность