В решении.
Пошаговое объяснение:
7. Побудуйте графік функції y = x²+4x-13. За графіком знайдіть: 3) область значення функції; 4) проміжки зростання та спадання функції.
7. Постройте график функции y = x² + 4x - 13.
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -6 -4 -2 0 2 1
у -1 -13 -17 -13 -1 19
По вычисленным точкам построить параболу.
По графику найдите:
3) область значения функции;
Область значений - это проекция графика на ось Оу.
Обозначается как Е(f) или Е(y).
Область значений параболы определяется координатами вершины, конкретно у₀, значение у вершины параболы.
Согласно графика, у₀ = -17.
Е(y) = у∈(-17; +∞).
4) промежутки возрастания и убывания функции.
Функция возрастает при х∈(-2; +∞);
Функция убывает при х∈(-∞; -2).
До чего ленивая молодежь пошла, им уже даже пишут, какие правила использовать, а они... Не учатся ничему и учиться не хотят... :)
1) Производная произведения:
Правило дифференцирования сложной функции: (индекс внизу означает, по какой переменной дифференцируем, * означает умножение)
тогда
2) Дифференцирование сложной функции
Примем
Дифференцируем f(g):
Дифференцируем g(x):
Тогда
3) Как и в 2, дифференцируем сложную функцию
4) Производная суммы есть сумма производных:
Окончательно
5) Опять производная сложной функции:
В решении.
Пошаговое объяснение:
7. Побудуйте графік функції y = x²+4x-13. За графіком знайдіть: 3) область значення функції; 4) проміжки зростання та спадання функції.
7. Постройте график функции y = x² + 4x - 13.
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -6 -4 -2 0 2 1
у -1 -13 -17 -13 -1 19
По вычисленным точкам построить параболу.
По графику найдите:
3) область значения функции;
Область значений - это проекция графика на ось Оу.
Обозначается как Е(f) или Е(y).
Область значений параболы определяется координатами вершины, конкретно у₀, значение у вершины параболы.
Согласно графика, у₀ = -17.
Е(y) = у∈(-17; +∞).
4) промежутки возрастания и убывания функции.
Функция возрастает при х∈(-2; +∞);
Функция убывает при х∈(-∞; -2).
До чего ленивая молодежь пошла, им уже даже пишут, какие правила использовать, а они... Не учатся ничему и учиться не хотят... :)
Пошаговое объяснение:
1) Производная произведения: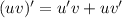
Правило дифференцирования сложной функции: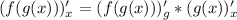 (индекс внизу означает, по какой переменной дифференцируем, * означает умножение)
(индекс внизу означает, по какой переменной дифференцируем, * означает умножение)
тогда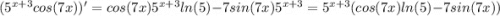
2) Дифференцирование сложной функции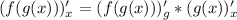
Примем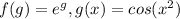
Дифференцируем f(g):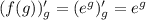
Дифференцируем g(x):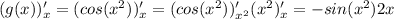
Тогда
3) Как и в 2, дифференцируем сложную функцию
4) Производная суммы есть сумма производных:
Окончательно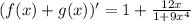
5) Опять производная сложной функции: