Конденсатор ёмкостью Q = 1мкФ включается в цепь( в момент времени t0 =0) с напряжением U=16В и сопротивлением R=520 Ом . Определить заряд q конденсатора в момент t =10с после включения.
Если число является двузначным (или однозначным), то утверждение очевидно.
Если число является трехзначным (или "более -значным"), то оно представимо в виде (где - соответствующее натуральное число, а - однозначное / двузначное число, образующееся двумя последними цифрами исходного числа).
Заметим, что: . Так что всегда делится на . И если тоже делится на , то искомое число, как сумма двух чисел, делящихся на ( и ), тоже будет делиться на .
Чтобы число делилось на 4, оно должно два раза подряд разделиться на 2, т.е. в разложении такого числа на простые множители д.б. 2². Чтобы число делилось на 6, оно должно делиться на 2 и на 3, т.е. в разложении числа на простые множители д.б. 2×3. Отсюда следует, что число будет делиться на 4 и на 6, если в его разложении на простые множители д.б. как минимум следующие множители: 2×2×3. Но это произведение равно 12. Число 12 как раз и делится на 4 и на 6, но не делится на 24. И таких чисел бесконечное множество. Например, 84 и 36.
Так что, утверждение НЕ ВЕРНО.
ЗЫ. Кстати, для доказательства, что утверждение неверно, достаточно было привести один опровергающий пример.
48 : 4 = 12 (48 : 4 = 12)
92 : 4 = 23 (92 : 4 = 23)
184 : 4 = 46 (84 : 4 = 21)
996 : 4 = 249 (96 : 4 = 24)
1236 : 4 = 309 (36 : 4 = 9)
5556 : 4 = 1389 (56 : 4 = 14)
Доказательство:Если число является двузначным (или однозначным), то утверждение очевидно.
Если число является трехзначным (или "более -значным"), то оно представимо в виде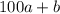 (где
(где  - соответствующее натуральное число, а
- соответствующее натуральное число, а 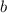 - однозначное / двузначное число, образующееся двумя последними цифрами исходного числа).
- однозначное / двузначное число, образующееся двумя последними цифрами исходного числа).
Заметим, что: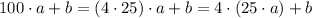 . Так что
. Так что 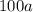 всегда делится на
всегда делится на 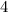 . И если
. И если 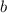 тоже делится на
тоже делится на 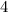 , то искомое число, как сумма двух чисел, делящихся на
, то искомое число, как сумма двух чисел, делящихся на 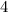 (
(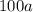 и
и 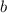 ), тоже будет делиться на
), тоже будет делиться на 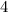 .
.
Утверждение доказано!
Чтобы число делилось на 6, оно должно делиться на 2 и на 3, т.е. в разложении числа на простые множители д.б. 2×3.
Отсюда следует, что число будет делиться на 4 и на 6, если в его разложении на простые множители д.б. как минимум следующие множители: 2×2×3. Но это произведение равно 12.
Число 12 как раз и делится на 4 и на 6, но не делится на 24. И таких чисел бесконечное множество. Например, 84 и 36.
Так что, утверждение НЕ ВЕРНО.
ЗЫ. Кстати, для доказательства, что утверждение неверно, достаточно было привести один опровергающий пример.