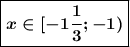ОДЗ : 1) x²+2>0 ⇒ x∈R
2) x²-x+12>0 ⇒ D=1-4·12=-47<0 ⇒ x∈R
3)
ОДЗ : x ∈ (-∞; -1) ∪ (0; +∞)
x² - x + 12 > 0 всегда, так как D < 0 ⇒
Метод интервалов : x₁ = ; x₂ = 0
+++++++++++ ----------- (0) +++++++++++> x
С учётом ОДЗ :
ОДЗ : 1) x²+2>0 ⇒ x∈R
2) x²-x+12>0 ⇒ D=1-4·12=-47<0 ⇒ x∈R
3)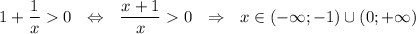
ОДЗ : x ∈ (-∞; -1) ∪ (0; +∞)
x² - x + 12 > 0 всегда, так как D < 0 ⇒
Метод интервалов : x₁ =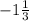 ; x₂ = 0
; x₂ = 0
+++++++++++![[-1\frac{1}{3}]](/tpl/images/0919/4650/98da6.png) ----------- (0) +++++++++++> x
----------- (0) +++++++++++> x
С учётом ОДЗ :