Начертите многоугольник с площадью 19 см² 50 ! ​

Пошаговое объяснение:

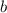Необходимо найти неизвестные переменные и , если их сумма 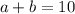, а отношение .

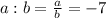Из определения частного мы получаем, что будет равно 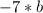, так как чтобы найти делимое, нужно итог деления или частное умножить на делитель. Получили: .

Подставим данное выражение в сумму двух переменных и найдём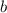 . Так как при нахождении неизвестной делитель получился отрицательным, то при делении мы имеем право минус вынести за дробь:

Нашли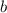 , поэтому данное значение в любое из выражений, найдем . Подставим во второе:

- нашли .

Сделаем проверку:

- все сходится.

Пошаговое объяснение:

у=х⁴-4х³-8х²+12

1) Область определения функции.

D(f) = R

2) Находим производную функции.

у' = 4х³-12х²-16х

3)Найдем нули производной:

y' = 0;

4х³-12х²-16х=0

4х(х²-3х-4)=0,

х₁=0, х₂=4 , х₃=-1 - критические точки (точки экстремума)

4) Получилось четыре промежутка:

(-∞; -1), (-1;0), (0; 4) и (4; +∞).

5) Расставим знаки производной на каждом промежутке:

(-∞; -1) если х = -2: y'(-2) = -8(4+6-4)= <0 (минус).

(-1;0) если х = 1: y'(-0,5) = -2(0,25+1,5-4) = 4,5 >0 (плюс).

(0; 4) если х = 1: y'(1) = 4(1-3-4) <0 (минус).

(4; +∞) если х = 5: y'(5) = 20(25-15-4) >0 (плюс).

6)Определяем промежутки возрастания и убывания функции

Если знак производной функции на промежутке положительный, то функция возрастает, если отрицательный - то убывает.

Функция возрастает (производная плюс) на х∈ (-1;0), (4;+∞)

Функция убывает на х∈ (-∞; -1) и (0;4;)

точка минимума функции х=-1; 4; точка максимума функции х=0.

f(x) max = f(0) = 12, минимум (0;12)

f(x) min =f(-1) = (-1)⁴-4*(-1)³-8*(-1)²+12 = 1+4-8+12=9

f(x) min =f(4) = (4)⁴-4*(4)³-8*(4)²+12=256-256-128+12=116

максимум (-1;9), (4; -116)