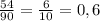А) sinxcosx+√3 cos^2x=0 cosx(sinx+√3cosx)=0 произведение двух сомножителей равно нулю тогда, когда хотя бы один из множителей равен 0, а другой при этом существует cosx=0 x=Π/2+Πn, n€Z sinx+√3cosx=0 | : на cosx tgx+√3=0 tgx=-√3 x=-Π/3+Πk, k€Z ответ: -Π/3+Πk, k€Z; Π/2+Πn, n€Z б) cos2x+9sinx+4=0 1-2sin^2x+9sinx+4=0 -2sin^2x+9sinx+5=0 Пусть t=sinx, где t€[-1;1], тогда -2t^2+9t+5=0 D=81+40=121 t1=-9-11/-4=5 посторонний корень t2=-9+11/-4=-1/2 Вернёмся к замене sinx=-1/2 x1=-5Π/6+2Πn, n€Z x2=-Π/6+2Πn, n€Z ответ: -5Π/6+2Πn, -Π/6+2Πn, n€Z
Количество двузначных чисел от 10 до 99 составляет 90.
Числа, которые делятся на 2, это числа которые оканчиваются цифрами 0, 2, 4, 6 или 8.
Числа, которые делятся на 5, это числа которые оканчиваются цифрой 0 или 5.
Числа, которые делятся на 2 и 5, это числа которые оканчиваются цифрой 0.
Таким образом, среди каждого десятка двузначных чисел количество чисел, которые подходят под критерии, а именно оканчиваются на одну из цифр 0, 2, 4, 5, 6, 8, составляет 6 штук. Например, в десятке чисел от 30 до 39, на 2 делятся 30, 32, 34, 36, 38, а на 5 делится 35, и на 2 и 5 делится 30, то есть подходящие под нужный критерий числа - это числа 30, 32, 34, 35, 36, 38, всего 6 штук.
Так как всего двузначных чисел 90, то есть 9 десятков, то подходящих чисел будет 9*6 = 54.
По классическому определению вероятности, вероятность того , что наудачу взятое двухзначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно составляет
cosx(sinx+√3cosx)=0
произведение двух сомножителей равно нулю тогда, когда хотя бы один из множителей равен 0, а другой при этом существует
cosx=0
x=Π/2+Πn, n€Z
sinx+√3cosx=0 | : на cosx
tgx+√3=0
tgx=-√3
x=-Π/3+Πk, k€Z
ответ: -Π/3+Πk, k€Z; Π/2+Πn, n€Z
б) cos2x+9sinx+4=0
1-2sin^2x+9sinx+4=0
-2sin^2x+9sinx+5=0
Пусть t=sinx, где t€[-1;1], тогда
-2t^2+9t+5=0
D=81+40=121
t1=-9-11/-4=5 посторонний корень
t2=-9+11/-4=-1/2
Вернёмся к замене
sinx=-1/2
x1=-5Π/6+2Πn, n€Z
x2=-Π/6+2Πn, n€Z
ответ: -5Π/6+2Πn, -Π/6+2Πn, n€Z
0,6
Пошаговое объяснение:
Количество двузначных чисел от 10 до 99 составляет 90.
Числа, которые делятся на 2, это числа которые оканчиваются цифрами 0, 2, 4, 6 или 8.
Числа, которые делятся на 5, это числа которые оканчиваются цифрой 0 или 5.
Числа, которые делятся на 2 и 5, это числа которые оканчиваются цифрой 0.
Таким образом, среди каждого десятка двузначных чисел количество чисел, которые подходят под критерии, а именно оканчиваются на одну из цифр 0, 2, 4, 5, 6, 8, составляет 6 штук. Например, в десятке чисел от 30 до 39, на 2 делятся 30, 32, 34, 36, 38, а на 5 делится 35, и на 2 и 5 делится 30, то есть подходящие под нужный критерий числа - это числа 30, 32, 34, 35, 36, 38, всего 6 штук.
Так как всего двузначных чисел 90, то есть 9 десятков, то подходящих чисел будет 9*6 = 54.
По классическому определению вероятности, вероятность того , что наудачу взятое двухзначное число окажется кратным либо 2, либо 5, либо тому и другому одновременно составляет