В швейную мастерскую привезли первый раз 4/9 количества сатина, намеченного по плану, во второй раз привезли 1/5 часть оставшегося, а в третий раз - остальные 112 м сатина. Со всего полученного сатина мастерская сшила 30 платьев и 44 рубашки. На каждое платье ушло сатина на 1 м больше, чем на каждую рубашку. Сколько сатина пошло отдельно на одно платье и на одну рубашку?
1)
2) от = привезли во 2 раз
3) - привезли за 2 первых раза.
4) привезли в третий раз.
5) (м) - всего сатина.
Пусть х (м) пошло на одну рубашку, тогда
(х+1) (м) пошло на одно платье
Уравнение:
3 м пошло на одну рубашку;
3+1 = 4 м пошло на одно платье
ответ: 4 м сатину пішло на одне плаття і 3 м на одну сорочку.
ответ: Обозначим через х число книг, которые стояли на первой полке первоначально.
Согласно условию задачи, на двух полках книг было поровну, следовательно, на второй полке также было х книг.
Согласно условию задачи, после того, как с первой полки сняли 8 книг, а со второй полки сняли 24 книги, на первой полке стояло книг в 3 раза больше, чем на второй, следовательно, можем составить следующее уравнение:
х - 8 = 3 * (х - 24).
Решаем полученное уравнение:
х - 8 = 3х - 72;
3х - х = 72 - 8;
2х = 64;
х = 64 / 2;
х = 32.
ответ: на каждой полке сначала было по 32 книги. СМОЖЕШЬ ВОТ ОБРАЗЕЦ??
В швейную мастерскую привезли первый раз 4/9 количества сатина, намеченного по плану, во второй раз привезли 1/5 часть оставшегося, а в третий раз - остальные 112 м сатина. Со всего полученного сатина мастерская сшила 30 платьев и 44 рубашки. На каждое платье ушло сатина на 1 м больше, чем на каждую рубашку. Сколько сатина пошло отдельно на одно платье и на одну рубашку?
1)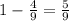
2)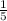 от
от 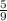 =
= 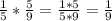 привезли во 2 раз
привезли во 2 раз
3)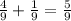 - привезли за 2 первых раза.
- привезли за 2 первых раза.
4)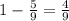 привезли в третий раз.
привезли в третий раз.
5)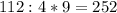 (м) - всего сатина.
(м) - всего сатина.
Пусть х (м) пошло на одну рубашку, тогда
(х+1) (м) пошло на одно платье
Уравнение:
3 м пошло на одну рубашку;
3+1 = 4 м пошло на одно платье
ответ: 4 м сатину пішло на одне плаття і 3 м на одну сорочку.
ответ: Обозначим через х число книг, которые стояли на первой полке первоначально.
Согласно условию задачи, на двух полках книг было поровну, следовательно, на второй полке также было х книг.
Согласно условию задачи, после того, как с первой полки сняли 8 книг, а со второй полки сняли 24 книги, на первой полке стояло книг в 3 раза больше, чем на второй, следовательно, можем составить следующее уравнение:
х - 8 = 3 * (х - 24).
Решаем полученное уравнение:
х - 8 = 3х - 72;
3х - х = 72 - 8;
2х = 64;
х = 64 / 2;
х = 32.
ответ: на каждой полке сначала было по 32 книги. СМОЖЕШЬ ВОТ ОБРАЗЕЦ??