Пусть х см - ширина прямоугольника. Тогда, (х+4) см - длина прямоугольника. Составим уравнение:
Раскроем скобки и перенесем все в левую часть:
Решать уравнение будем по формуле корней для уравнения с четным вторым коэффициентом:
Поскольку сторона не может выражаться отрицательным числом, то первый корень не удовлетворяет условию задачи. Тогда:
- ширина прямоугольника
- длина прямоугольника
Составим выражения для периметра:
Находим периметр:
ответ: стороны прямоугольника 6 см и 10 см; периметр прямоугольника 32 см
Пошаговое объяснение:
Уравнение параболы в общем виде записывается следующим образом:
где , и -- коэффициенты, которые нам необходимо найти.
Подставим известные нам точки в уравнение параболы и составим систему из трёх уравнений:
Эту систему можно решать по-разному, дело вкуса. Даю простейшее решение с выражением каждого неизвестного по-очереди.
Умножим второе уравнение на 2 и вычтем из третьего второе, чтобы избавиться от :
Отсюда видно, что , получаем из второго уравнения, а из первого:
Таким образом, - уравнение нашей параболы.
Пусть х см - ширина прямоугольника. Тогда, (х+4) см - длина прямоугольника. Составим уравнение:
Раскроем скобки и перенесем все в левую часть:
Решать уравнение будем по формуле корней для уравнения с четным вторым коэффициентом:
Поскольку сторона не может выражаться отрицательным числом, то первый корень не удовлетворяет условию задачи. Тогда:
- ширина прямоугольника
- длина прямоугольника
Составим выражения для периметра:
Находим периметр:
ответ: стороны прямоугольника 6 см и 10 см; периметр прямоугольника 32 см
Пошаговое объяснение:
Уравнение параболы в общем виде записывается следующим образом:
где ,
, 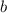 и
и  -- коэффициенты, которые нам необходимо найти.
-- коэффициенты, которые нам необходимо найти.
Подставим известные нам точки в уравнение параболы и составим систему из трёх уравнений:
Эту систему можно решать по-разному, дело вкуса. Даю простейшее решение с выражением каждого неизвестного по-очереди.
Умножим второе уравнение на 2 и вычтем из третьего второе, чтобы избавиться от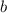 :
:
Отсюда видно, что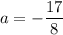 ,
, 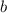 получаем из второго уравнения, а
получаем из второго уравнения, а  из первого:
из первого:
Таким образом,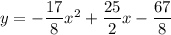 - уравнение нашей параболы.
- уравнение нашей параболы.