2
Пошаговое объяснение:
Если неравенство выполняется для всех значений x, то оно выполняется и для x=1-p: Тогда максимально возможное целое значение, которое может принимать p, равно 2. Проверим, удовлетворяет ли оно условию.
- Верно.
2
Пошаговое объяснение:
Если неравенство выполняется для всех значений x, то оно выполняется и для x=1-p: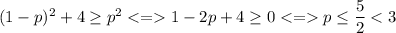 Тогда максимально возможное целое значение, которое может принимать p, равно 2. Проверим, удовлетворяет ли оно условию.
Тогда максимально возможное целое значение, которое может принимать p, равно 2. Проверим, удовлетворяет ли оно условию.
- Верно.