, то есть это круг (с границей), с центром в точке и радиусом . Среди точек этого множества требуется найти такие, для которых принимает наибольшее значение. Понятно также, что никакая точка внутренности не является искомой, поскольку ее можно сдвинуть на вектор для некоторого . Потому точки ищем на границе.
Рассмотрим прямую . Требуется максимизировать , то есть увеличивать это значение до тех пор, пока эта прямая имеет пересечения с окружностью. Предельный случай -- касание. Имеем: , , откуда . Тогда и .
Рассмотрим прямую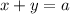
. Требуется максимизировать 
, то есть увеличивать это значение до тех пор, пока эта прямая имеет пересечения с окружностью. Предельный случай -- касание. Имеем: 
, 
, откуда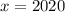 
. Тогда 
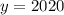и 
.