Пусть первый спортсмен вернулся к месту старта через x минут после начала своего заплыва. x мин = 60x секунд.
Значит, от одного другого конца бассейна первый доплывает за 60x:2 = 30x секунд.
Пусть длина дорожки y метров (можно и за единицу принять - всё равно сократится потом).
Тогда м/с скорость первого пловца, м/с - скорость второго.
От конца дорожки до места встречи первый доплыл за 30x-25 секунд. Второй от начала дорожки до места встречи доплыл за то же время, т.к. начали встречное движение одновременно.
За это время первый проплыл метров, второй метров. В сумме проплыли расстояние, равное длине дорожки, то есть
ответ: первый спортсмен вернулся к месту старта через 1,5 минуты после начала своего заплыва
Даны вершины пирамиды A(2,-3,5), B(0,2,1), C(-2,-2,3),D(3,2,4).
Будем считать, что требуется определить высоту из точки Д.
Находим векторы АВ и АС для определения площади основания АВС.
АВ = (-2; 5; -4), АС = (-4; 1; -2).
Их векторное произведение равно.
i j k | i j
-2 5 -4 | -2 5
-4 1 -2 | -4 1 = -10i + 16j - 2k - 4j + 4i + 20k = -6i + 12j + 18k.
Площадь грани ABС равна половине модуля полученного векторного произведения (-6; 12; 18).
S(ABСD) = (1/2)*√(36 + 144 + 324) = (1/2)√504= 3√14 ≈ 11,225.
Находим вектор АD = (1; 5; -1).
Объём пирамиды равен (1/6) смешанного произведения (АВхАС)*АД.
(АВхАС) = (-6; 12; 18), АД = (1; 5; -1).
V = (1/6)*(-6*1 + 12*5 + 18*(-1)) = 36/6 = 6 куб.ед.
Теперь можно определить высоту ДН из точки Д на основание АВС.
ДН = 3V/S(ABC) = 3*6/(3√14) = 3√14 / 7 ≈ 1,6036.
Пусть первый спортсмен вернулся к месту старта через x минут после начала своего заплыва. x мин = 60x секунд.
Значит, от одного другого конца бассейна первый доплывает за 60x:2 = 30x секунд.
Пусть длина дорожки y метров (можно и за единицу принять - всё равно сократится потом).
Тогда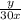 м/с скорость первого пловца,
м/с скорость первого пловца, 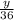 м/с - скорость второго.
м/с - скорость второго.
От конца дорожки до места встречи первый доплыл за 30x-25 секунд. Второй от начала дорожки до места встречи доплыл за то же время, т.к. начали встречное движение одновременно.
За это время первый проплыл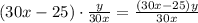 метров, второй
метров, второй 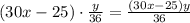 метров. В сумме проплыли расстояние, равное длине дорожки, то есть
метров. В сумме проплыли расстояние, равное длине дорожки, то есть
ответ: первый спортсмен вернулся к месту старта через 1,5 минуты после начала своего заплыва