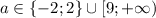Пусть . Показательная функция — монотонно возрастающая, поэтому на количестве корней эта замена не сказывается (кроме t ≤ 0). Тогда
Заметим, что второй корень всегда положителен, то есть как минимум один корень у этого уравнения есть. Тогда другой корень должен быть либо неположительным, либо совпасть с первым.
Пошаговое объяснение:
Пусть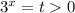 . Показательная функция — монотонно возрастающая, поэтому на количестве корней эта замена не сказывается (кроме t ≤ 0). Тогда
. Показательная функция — монотонно возрастающая, поэтому на количестве корней эта замена не сказывается (кроме t ≤ 0). Тогда
Заметим, что второй корень всегда положителен, то есть как минимум один корень у этого уравнения есть. Тогда другой корень должен быть либо неположительным, либо совпасть с первым.
В первом случае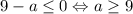 .
.
Во втором случае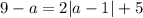
Если a ≥ 1, то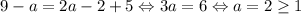
Если a < 1, то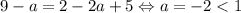
Таким образом,