Найдите значение выражения:
а) 2sin120° - sin90° - tg60°;
б)3sin^2π/6+2cos^2(−π)- ctg^2(π/6)
Найти производную функции:
y = 4x^3 − 2x + 2

Показать ответ

Ответ:

ivantitov2002

07.10.2021 23:20

Это зависит от количества долек в плитке. Одного размера плитки недостаточно.
Предположим, что размер дольки 2 на 3 см и всего долек в плитке 25.
Эту плитку можно разломать на дольки за 24 хода.
Следовательно, выиграет тот, кто не начинает.

Если размер долек 2 на 1,5 см, то количество долек 50 и разломать плитку на дольки можно за 49 ходов. В этом случае выиграет тот, кто начинает.

Вообще, ходов на разламывание всей плитки на дольки нужно на 1 меньше, чем количество долек. Если это количество четное, то выигрывает тот, кто начинает, если нечетное, то выигрывает тот, кто ходит вторым.

0,0(0 оценок)

Ответ:

Theyom47

17.09.2020 21:29

ответ: 360 км.

Пошаговое объяснение:

Пусть расстояние между А и В равно z км, а скорость пассажирского и товарного поездов равна х км/ч и у км/ч соответственно. Тогда время, затраченное пассажирским поездом на преодоления пути равно z/x (ч), а товарным — z/y (ч), что на 3+12/60 ч больше по условию. Имеем первое уравнение системы: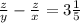 $\frac{z}{y} - \frac{z}{x} =3 \frac{1}{5}$

За z/y (ч) пассажирский поезд проедет (z+288) км. Имеем второе уравнение системы: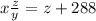 $x\frac{z}{y} = z + 288$

После повышения скорости на 10 км/ч пассажирский поезд потратит на путь (z/(x+10)) ч, а товарный — (z/(y+10)) ч, что на 2+24/60 ч больше по условию. Имеем третье уравнение системы:

$\frac{z}{y+10} - \frac{z}{x+10} = 2\frac{2}{5}$