пусть u=5-7
Тогда du=-7dx и подставляем Получим:
Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:
Интеграл от синуса есть минус косинуса:
Таким образом, результат будет: а, если сейчас заменить u еще в:
Добавляем постоянную интегрирования;
ответ;
Либо
Пошаговое объяснение:
пусть u=5-7
Тогда du=-7dx и подставляем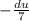 Получим:
Получим:
Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:
Интеграл от синуса есть минус косинуса:
Таким образом, результат будет: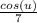 а, если сейчас заменить u еще в:
а, если сейчас заменить u еще в:
Добавляем постоянную интегрирования;
ответ;
Либо
Пошаговое объяснение: