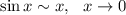Войти Регистрация Спроси ai-bota

Найти предел, не используя правило лопиталя

Показать ответ

Ответ:

boatengknhalotldze

10.10.2020 23:48

эквивалентность функции $\displaystyle \sin x\sim x,~~x\to 0$

$\displaystyle \lim_{x \to \frac{\pi}{6}}\dfrac{\sin\left(x^2-\dfrac{\pi^2}{36}\right)}{\dfrac{\sqrt{3}}{2}-\cos x}=\lim_{x \to \frac{\pi}{6}}\dfrac{x^2-\dfrac{\pi^2}{36}}{\cos\dfrac{\pi}{6}-\cos x}=\lim_{x \to \frac{\pi}{6}}\dfrac{x^2-\dfrac{\pi^2}{36}}{-2\sin\dfrac{\frac{\pi}{6}+x}{2}\sin\dfrac{\frac{\pi}{6}-x}{2}}=\\ \\ \\ =-\dfrac{1}{2}\lim_{x \to \frac{\pi}{6}}\dfrac{\left(x-\dfrac{\pi}{6}\right)\left(x+\dfrac{\pi}{6}\right)}{\sin\dfrac{\frac{\pi}{6}+x}{2}\cdot \dfrac{\frac{\pi}{6}-x}{2}}=\dfrac{1}{2}\lim_{x \to \frac{\pi}{6}}\dfrac{x+\dfrac{\pi}{6}}{\sin\dfrac{\frac{\pi}{6}+x}{2}}=\dfrac{1}{2}\cdot \dfrac{\dfrac{\pi}{6}+\dfrac{\pi}{6}}{\sin \dfrac{\pi}{6}}=\dfrac{2\pi}{3}$

0,0(0 оценок)

Популярные вопросы: Математика

irynks468dig

02.12.2022 11:44

Сплавили два свинцовых шара с радиусами 5 см и 7 см. найдите диаметр получившегося шара. ответ округлите до десятых...

enni00

02.12.2022 11:44

4^(х+1)+19*2^x-5=0 , где 4^(х+1) 4 в степени х+1,а 2^x 2 в степени х...

rusibragimova9

02.12.2022 11:44

Вавтобусе ехали 47 пассажиров. на остановке 12 пассажиров вышли и 9 вошли. сколько стало пассажиров в автобусе...

stanislavovichs

02.12.2022 11:44

2.найдите точку минимума функции у=(9-x)e9-x 3.найдите наименьшее значение функции у=4cosx+13x+9 на отрезке (0; 3π/2) 4.решить уравнение (cos2x-cosx+1)/(2sinx-√3)=0 , кто...

alisabugor

21.04.2020 01:30

Зараниє у двох цехах164 робітникив.скільки людей працює в кожному цеху,якщо у першому цеху робітників у 3 рази більше ніж у другому....

tisha199567

21.04.2020 01:30

Решить показательное неравенство (1/2)^х≥1/16...

ArtemS99

21.04.2020 01:30

Для функции f(x)=3+x2 найдите первообразную, график которой проходит через данную точку m(-1,6)...

mariaa987

21.04.2020 01:30

Вокружности с центром o ac и bd - диаметры. центральный угол aod равен 44. найдите вписанный угол acb...

alinkass

21.04.2020 01:30

Аня выше юли. виктор ниже ани. какое из утверждений самое точное? виктор выше юли виктор ниже юли виктор такого же роста как и юля ответить точно не возможно...

Lezgin228

21.04.2020 01:30

Впервый день туристы преодолели 38.7 км что составляет 14% всего пути. сколько км составляет весь намеченный путь?...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку