Геометрический смысл определенного интеграла - площадь фигуры под графиком функции. Таким образом, задача сводится к вычислению определенного интеграла. Сначала следует определить пределы интегрирования. Для этого нужно найти пересечения кривой с осью x (y=0):
Геометрический смысл определенного интеграла - площадь фигуры под графиком функции. Таким образом, задача сводится к вычислению определенного интеграла. Сначала следует определить пределы интегрирования. Для этого нужно найти пересечения кривой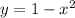 с осью x (y=0):
с осью x (y=0):
Получаем такой интеграл: