По кругу сидят мальчики и девочки. Известно, что количество сидящих рядом пар детей одного пола равно количеству сидящих рядом пар разного пола. Докажите, что общее количество детей делится на 4.
Пусть мальчики и девочки образуют многоугольник (2-регулярный граф). Ребро, соединяющее две вершины, покрасим в черный, если две вершины одного пола, и белым в обратном случае. Пусть девочка закодирована числом 0, а мальчик — 1.
Нетрудно видеть, что граф разделился на чередующиеся островки белого и черного. На концах черных островков стоят одинаковые числа. Сумма концов черных островков четна. Поэтому сумма концов белых островков тоже четна. Рассмотрим два вида белых островков — те, что содержат четное количество ребер, и те, что содержат нечетное их количество. Нечетные белые островки имеют начало и конец в разных цифрах, а поскольку сумма цифр четна, то нечетных белых островков четное количество.
Пусть — суммарное количество белых островков, а — суммарное количество черных. По условию , значит, четно. Всего ребер, что равно — делится на 4. Количество ребер совпадает с количеством детей.
Пусть мальчики и девочки образуют многоугольник (2-регулярный граф). Ребро, соединяющее две вершины, покрасим в черный, если две вершины одного пола, и белым в обратном случае. Пусть девочка закодирована числом 0, а мальчик — 1.
Нетрудно видеть, что граф разделился на чередующиеся островки белого и черного. На концах черных островков стоят одинаковые числа. Сумма концов черных островков четна. Поэтому сумма концов белых островков тоже четна. Рассмотрим два вида белых островков — те, что содержат четное количество ребер, и те, что содержат нечетное их количество. Нечетные белые островки имеют начало и конец в разных цифрах, а поскольку сумма цифр четна, то нечетных белых островков четное количество.
Пусть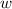 — суммарное количество белых островков, а
— суммарное количество белых островков, а 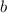 — суммарное количество черных. По условию
— суммарное количество черных. По условию 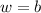 , значит,
, значит, 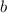 четно. Всего
четно. Всего 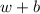 ребер, что равно
ребер, что равно 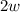 — делится на 4. Количество ребер совпадает с количеством детей.
— делится на 4. Количество ребер совпадает с количеством детей.