Натуральные числа (N) - те целые числа, что мы используем при счёте, не включая 0. Т.е. N={1, 2, 3, 4, 5, 6...} Выпишем такие элементы из множества А в подмножество В.
В={5}
Записывается это так: В⊂А (В включено в А, или В - часть множества А, В - подмножество множества А)
Целые числа (Z) - это множество значений координатной прямой, которые имеют вид a,(0), т.е. все натуральные числа, нуль и все отрицательные числа. Выпишем такие элементы из множества А в подмножество С.
С={-4; 0; 5}
Запишем, как С⊂А (С включено в А, или С - часть множества А, С - подмножество множества А)
Рациональные числа (Q) - это подмножество множества действительных чисел, которые можно записать в виде дроби . Иными словами, все приведённые в множестве А значения входят в множество рациональных чисел. Значит, множество А полностью соответствует множеству D.
поровну
Пошаговое объяснение:
По порядку
было 100% кофе, отпил 50% кофе, осталось 50% кофе, долил 50% молока
было 50/50, отпил 33% каждого, осталось 33% кофе и 33% молока, долил 33% молока
было 33/66, отпил 1/6 каждого, осталось 27.777% кофе и 55.555 молока, долил 16.666% молока
было 27.777/72.222, выпил все
всего кофе выпито:
0.5л+0.333х0.5л+0.166х0.333л+0.277л=1л, как ни крути, а выпил он все кофе, которое было изначально
всего молока выпито:
0.33х0.5л+0.166х0.666л+0.722л=1л
получается поровну, что и логично, т.к. он подливал ровно столько молока, сколько выпивал кофе
Или еще проще, с использованием дробей: кофе выпил 1 полный стакан, а молока 1/2+1/3+1/6, что в сумме также дает 1 полный стакан
Натуральные числа (N) - те целые числа, что мы используем при счёте, не включая 0. Т.е. N={1, 2, 3, 4, 5, 6...} Выпишем такие элементы из множества А в подмножество В.
В={5}
Записывается это так: В⊂А (В включено в А, или В - часть множества А, В - подмножество множества А)
Целые числа (Z) - это множество значений координатной прямой, которые имеют вид a,(0), т.е. все натуральные числа, нуль и все отрицательные числа. Выпишем такие элементы из множества А в подмножество С.
С={-4; 0; 5}
Запишем, как С⊂А (С включено в А, или С - часть множества А, С - подмножество множества А)
Рациональные числа (Q) - это подмножество множества действительных чисел, которые можно записать в виде дроби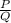 . Иными словами, все приведённые в множестве А значения входят в множество рациональных чисел. Значит, множество А полностью соответствует множеству D.
. Иными словами, все приведённые в множестве А значения входят в множество рациональных чисел. Значит, множество А полностью соответствует множеству D.
Диаграмму представлю в прикрепе...