То что написано маленькими цифорками, это мы запоминаем единицы.
пример:
26•4.
1. когда6•4=24; чтобы не произошло путаницы, мы пишем только десятки (вторая цифра в числе), а значит: 4 пишем, 2 запоминаем (пишем сверху карандашом или ручкой), потому что число у нас двухзначное.
2. 2•4=8; тут у нас получилась цифра,
но есть одно но, у нас есть число 2 которое мы запомнили, с ним надо что-то сделать, и поэтому мы к числу 8 прибавляем 2, получается 10.
теперь мы просто пишем 10 слево от 4. (как показано на картинке)
тоже самое мы проделываем и с остальными примерами.
Определение. Назовём числом сочетаний из n по k число выбрать из множества мощностью n элементов множество мощностью k элементов, будем обозначать и определим формулой
Если нужно доказательство, пишите
Итак, приступаем к решению.
Сначала раздаем первому игроку.
Для него есть 32 карты, из которых мы выбираем 10. Тогда количество выбрать эти карты есть число сочетаний из 32 по 10.
Но можно было просто оставить
Мы уже дали 10 карт первому, поэтому осталось 32 - 10 = 22 карт.
Тогда количество раздать второму 10 карт из 22 - это
Или опять же можно было бы оставить
Третьему останется всего лишь 22 - 10 = 12 карт. Тогда точно также, число выбрать из 12 карт 10 равно
Ну хоть здесь нормальное число. Но опять же можно было и оставить
И так, для каждого из игроков есть свои варианты выбора, причем выбор другого, напрямую зависит от выбрав первого. Тогда нам необходимо перемножить все эти результаты.
подробное решение:
То что написано маленькими цифорками, это мы запоминаем единицы.
пример:
26•4.
1. когда6•4=24; чтобы не произошло путаницы, мы пишем только десятки (вторая цифра в числе), а значит: 4 пишем, 2 запоминаем (пишем сверху карандашом или ручкой), потому что число у нас двухзначное.
2. 2•4=8; тут у нас получилась цифра,
но есть одно но, у нас есть число 2 которое мы запомнили, с ним надо что-то сделать, и поэтому мы к числу 8 прибавляем 2, получается 10.
теперь мы просто пишем 10 слево от 4. (как показано на картинке)
тоже самое мы проделываем и с остальными примерами.
или
Пошаговое объяснение:
Давайте сначала введём понятие.
Определение. Назовём числом сочетаний из n по k число выбрать из множества мощностью n элементов множество мощностью k элементов, будем обозначать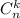 и определим формулой
и определим формулой
Если нужно доказательство, пишите
Итак, приступаем к решению.
Сначала раздаем первому игроку.
Для него есть 32 карты, из которых мы выбираем 10. Тогда количество выбрать эти карты есть число сочетаний из 32 по 10.
Но можно было просто оставить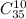
Мы уже дали 10 карт первому, поэтому осталось 32 - 10 = 22 карт.
Тогда количество раздать второму 10 карт из 22 - это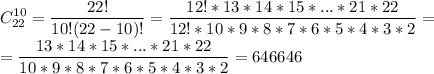
Или опять же можно было бы оставить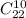
Третьему останется всего лишь 22 - 10 = 12 карт. Тогда точно также, число выбрать из 12 карт 10 равно
Ну хоть здесь нормальное число. Но опять же можно было и оставить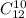
И так, для каждого из игроков есть свои варианты выбора, причем выбор другого, напрямую зависит от выбрав первого. Тогда нам необходимо перемножить все эти результаты.
Получим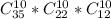
Или если в числах, то это