Разность чисел a и b делится на c, если a и b имеют равные остатки при делении на с.
Рассмотрим остатки от деления данного выражения на 5. 3 имеет остаток 3, поэтому 2ⁿ также должно иметь остаток 3. Заметим, что все числа вида имеют такой остаток. Докажем это методом математической индукции:
1. База индукции: при k = 1
2. Переход: пусть при k = x утверждение верно. Тогда при k = x + 1:
Утверждение доказано. Так как k — любое натуральное число, данных в условии чисел бесконечно много.
Аналогично 2ⁿ должно иметь остаток 3 при делении на 13. Также докажем по индукции, что числа вида подходят:
1. База индукции: при k = 1
2. Переход: пусть при k = x утверждение верно. Тогда при k = x + 1:
Утверждение доказано, данных в условии чисел, делящихся на 13, бесконечно много.
Докажем, что не существует чисел вида 2ⁿ, которые при делении на 65 дают остаток 3. Выпишем первые 12 остатков: 2 4 8 16 32 64 63 61 57 49 33 1. Среди них нет ни одной тройки. Докажем, что они повторяются, то есть , где k — неотрицательное целое число, 0 ≤ t ≤ 11 (за исключением случая k = t = 0):
— верно. Значит, 2ⁿ не может давать 3 при делении на 65.
В начале любого числа стоит ненулевая цифра. Пусть первая цифра равна 1. Тогда сумма цифр в числе равна 1 + 2 + 3 + 9 = 15. Чтобы сумма цифр стала равна 16, нужно все доступные разряды заменить на нули, но один из них заменить на единицу. Так как из 100 цифр занято 4, то существует разместить единицу среди оставшихся разрядов.
Пусть первая цифра равна 2. Тогда сумма цифр уже равна 16, все оставшиеся разряды возможно заменить только нулями. Получаем ещё одно подходящее число.
Если же первая цифра больше 2, то сумма цифр будет больше 16, эти варианты заведомо не подходят.
Разность чисел a и b делится на c, если a и b имеют равные остатки при делении на с.
Рассмотрим остатки от деления данного выражения на 5. 3 имеет остаток 3, поэтому 2ⁿ также должно иметь остаток 3. Заметим, что все числа вида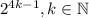
имеют такой остаток. Докажем это методом математической индукции:
1. База индукции: при k = 1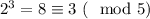
2. Переход: пусть при k = x утверждение верно. Тогда при k = x + 1:
Утверждение доказано. Так как k — любое натуральное число, данных в условии чисел бесконечно много.
Аналогично 2ⁿ должно иметь остаток 3 при делении на 13. Также докажем по индукции, что числа вида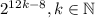
подходят:
1. База индукции: при k = 1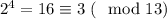
2. Переход: пусть при k = x утверждение верно. Тогда при k = x + 1:
Утверждение доказано, данных в условии чисел, делящихся на 13, бесконечно много.
Докажем, что не существует чисел вида 2ⁿ, которые при делении на 65 дают остаток 3. Выпишем первые 12 остатков: 2 4 8 16 32 64 63 61 57 49 33 1. Среди них нет ни одной тройки. Докажем, что они повторяются, то есть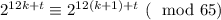
, где k — неотрицательное целое число, 0 ≤ t ≤ 11 (за исключением случая k = t = 0):
97
Пошаговое объяснение:
В начале любого числа стоит ненулевая цифра. Пусть первая цифра равна 1. Тогда сумма цифр в числе равна 1 + 2 + 3 + 9 = 15. Чтобы сумма цифр стала равна 16, нужно все доступные разряды заменить на нули, но один из них заменить на единицу. Так как из 100 цифр занято 4, то существует разместить единицу среди оставшихся разрядов.
Пусть первая цифра равна 2. Тогда сумма цифр уже равна 16, все оставшиеся разряды возможно заменить только нулями. Получаем ещё одно подходящее число.
Если же первая цифра больше 2, то сумма цифр будет больше 16, эти варианты заведомо не подходят.
Итого 97 подходящих чисел.