Предприниматель арендовал место на складе и ему на этот склад были доставлены 2000 посылок. У начальника склада есть стандартные формы распоряжений для охраны склада: "Удержать посылки №№" и "Отпустить посылки №№". Начальник склада и предприниматель играют в следующую игру: за один ход начальник вписывает произвольные номера посылок в одну такую форму, отдает предпринимателю, а предприниматель оставляет в ней одно из слов -- "удержать" или "отпустить". Далее, если предприниматель попросит, начальник склада выписывает новое распоряжение (номера посылок в нем могут совпадать с номерами посылок в предыдущих распоряжениях). Если в распоряжении остается слово "отпустить", то предприниматель забирает со склада все посылки, перечисленные в этой бумаге. Если же остается слово "удержать", то предприниматель забирает со склада все посылки, НЕ указанные в этой бумаге.
Какого количества таких бумаг предпринимателю гарантированно хватит, чтобы забрать все посылки со склада?
Другая сторона = (а + 2)см
Р = 2(а + а + 2)
28 = 2(2а + 2)
28 = 4а + 4
4а = 28 - 4
4а = 24
а = 6
а + 2 = 6 + 2 = 8
6 * 8 = 48 (кв.см) - площадь
ответ: 48кв.см - площадь прямоугольника
Теперь решение для 3-его класса без а:
Так как одна сторона на 2см меньше, то противоположная ей сторона
тоже меньше на 2 см.
Решение:
1) 2 + 2 = (на) 4см меньше был бы периметр прямоугольника и мы
получили бы квадрат
2) 28 - 4 = 24(см) - периметр квадрата был бы
3) 24 : 4 = 6(см) - сторона квадрата - это ширина прямоугольника
4) 6 + 2 = 8(см) - длина нашего прямоугольника
5) 6 * 8 = 48(кв.см)
ответ: тот же.
1) Начало ряда кратных 15 чисел: 15, 30, 45, 60, ...;
2) На 6-м месте в этом ряду стоит число 15 * 6 = 90;
3) На 10-м месте: 15 * 10 = 150;
4) На 40-м: 15 * 40 = 600.
Пошаговое объяснение:
Числа, кратные 15 - это числа, делящиеся на 15 (и если мы считаем, что ряд таких чисел имеет начало, то чаще всего имеются ввиду положительные числа, удовлетворяющие данному требованию). То есть их можно представить в виде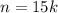
, где n - произвольное число этого ряда, k - произвольное натуральное число. Первое число этого ряда, естественно, примет вид 15 * 1 = 15, а за ним пойдут все числа, большие него на 15m (m - некое натуральное число).
Тогда перед нами арифметическая прогрессия с первым членом 15 и разностью 15, и любой ее член можно вычислить по формуле
, откуда и следуют все изложенные выше ответы.