Продолжи предложения а) из одной точки к плоскости проведены перпендикуляр и наклонная. углы, образованные наклонной с ее проекцией и с перпендикуляром, равны. угол между наклонной и плоскостью равен … б) ребро ас тетраэдра авсd перпендикулярно к плоскости грани всd, отрезок ah – высота грани abd. тогда bhc = … 3. справедливо ли утверждение? а) ed перпендикулярно ac,если ∆abc - равносторонний, то oe перпендикулярно (abc). б) ofперпендикулярно ef,если abcdef - правильный шестиугольник и obперпендикулярно (abf). 4. реши : 1. в ∆мkc, см перпендикулярно kм, т.е не принадлежит плоскости мкс и ем перпендикулярно мк, то а) км(мес); б) кмсе. 2. в ∆ авс, ав = 16 см, а = 30°, bк перпендикулярно (abc). расстояние от к до ас равно 17 см. найти вк. в 3. в ∆ авс с = 90°, ас = 8см, вс = 6 см. cdперпендикулярно (abc). найти cd, если расстояние от d до ав равно 5 см.

Показать ответ

Ответ:

Варенье11333333

06.06.2020 16:27

ответ: 180.

Вот формула площади трапеции:

$S = \frac{a + b}{2} *h$ , где a и b - основания трапеции, а h - высота (S, разумеется, площадь).

Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен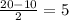 $\frac{20 - 10}{2} = 5$ . Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:

$a = \sqrt{c^2 - b^2} = \sqrt{13^2 - 5^2} = \sqrt{169-25} = \sqrt{144} = 12.$

Теперь высоту мы знаем и можем найти площадь трапеции:

$S = \frac{a + b}{2} * h = \frac{10+20}{2}*12 = \frac{30}{2}*12 = 15*12 = 180.$

Задача решена!

Основания равнобедренной трапеции равны 10 и 20, а её боковые сто-роны равны 13. найдите площадь тра

0,0(0 оценок)

Ответ:

Mas4323

10.02.2022 04:33

1) умножим обе части уравнения на 6,получим уравнение х²-х=12
х²-х-12=0
по т.виета находим корни х1+х2=1, х1*х2=-12.подбором находим корни х1=-5,х2=6 можно корни найти через дискриминант.
2) x²-x=2x-5
х²-х-2х+5=0
х²-3х+5=0
д=(-3)²-4*1*5=-11корней нет, так как д∠0
разложите, если возможно на множители многочленs:
x²+9x-10=(х+10)(х-1)
x²-2x-15=(х-5)(х+3)
чтобы разложить на множители многочлен второй степени ,нужно решить квадратное уравнение , полученные корни подставить в формулу
а(х-х1)(х-х2)

0,0(0 оценок)

Популярные вопросы: Математика