Рабочий обслуживает 4 автомата. Вероятность брака для первого автомата равна - 0,03, для второго - 0,02, для третьего - 0,04, для четвертого - 0,02. Производительность первого автомата в три раза больше чем второго, третьего в два раза меньше, чем второго, а четвертого равна производительности первого автомата. Изготовленные детали попадают на общий конвейер. Определить вероятность того, что взятая наудачу деталь будет бракованным.

Показать ответ

Ответ:

Lizzik657

21.10.2022 07:12

Найдем сначала общее решение соответствующего однородного уравнения:

y''+25y=0

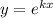Пусть $y=e^{kx}$ , получим характеристическое уравнение:

$k^2+25=0\\ k=\pm5i$

Характеристическое уравнение имеет два комплексных корня Два линейно независимые решения это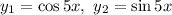 $y_1=\cos 5x,~ y_2=\sin5x$

Общее решение однородного дифференциального уравнения:

$y^*=y_1+y_2=C_1\cos 5x+C_2\sin5x$

Рассмотрим правую часть дифференциального уравнения:

$f(x)=e^{0x}(100x\sin5x+50\cos 5x)~~\Rightarrow~~~\alpha =0;~~~ \beta=5\\ P_n(x)=100x~~~\Rightarrow~~~ n=1;~~~ Q_n(x)=50~~~\Rightarrow~~~ n=0$

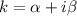Число $k=\alpha +i\beta$ принимает значение 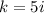k=5i , это число является корнем характеристическое уравнение 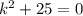k^2+25=0 . Кратность k=1

Частное решение будем искать в виде:

$y^{**}=x^{k}((Ax+B)\sin 5x+(Cx+D)\cos 5x)=\\ \\ =(Ax+B)x\sin 5x+(Cx+D)x\cos 5x$

Вычислим для нее производную второго порядка

$y'=\left(-5Cx^2+\left(2A-5D\right)x+D\right)\sin 5x+(5Ax^2+(5B+2C)x+D)\cos5x\\ \\ y''=(-25Ax^2-(25B+20C)x-10D+2A)\sin 5x+(-25Cx^2+\\ \\ +(20A-25D)x+10B+2C)\cos 5x$

Подставив в исходное дифференциальное уравнение, получим:

$(-20Cx-10D+2A)\sin 5x+(20Ax+10B+2C)\cos 5x=100x\sin 5x+50\cos5x$

Приравниваем коэффициенты при xcos5x, xsin5x, sin5x, cos5x, получим систему уравнений:

$\begin{cases}&\text{}2A-10D=0\\&\text{}10B+2C=50\\&\text{}-20C=100\\&\text{}20A=0\end{cases}~~~~\Longrightarrow~~~\begin{cases}&\text{}D=0\\&\text{}B=6\\&\text{}C=-5\\&\text{}A=0\end{cases}$

Частное решение: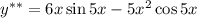 $y^{**}=6x\sin 5x-5x^2\cos 5x$

Общее решение линейного неоднородного дифференциального уравнения:

$y=y^*+y^{**}=C_1\cos 5x+C_2\sin5x+6x\sin 5x-5x^2\cos 5x$

0,0(0 оценок)

Ответ:

aytac200505

29.11.2022 21:10

По дороге зимней, скучной Тройка борзая бежит, Колокольчик однозвучный Утомительно гремит. Что-то слышится родное В долгих песнях ямщика: То разгулье удалое, То сердечная тоска Ни огня, ни черной хаты, Глушь и снег На встречу мне Только версты полосаты Попадаются одне... Скучно, грустно завтра, Нина, Завтра к милой возвратясь, Я забудусь у камина, Загляжусь не наглядясь. Звучно стрелка часовая Мерный круг свой совершит, И, докучных удаляя, Полночь нас не разлучит. Грустно, Нина: путь мой скучен, Дремля смолкнул мой ямщик, Колокольчик однозвучен, Отуманен лунный лик.

0,0(0 оценок)

Популярные вопросы: Математика