Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одномответ:
строгих неравенств
12 ноября 2017Материалы к урокуСкачать: [Домашнее задание] Домашнее заданиеСкачать: [ответы] ответыДля начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:(x − 5)(x + 3) > 0Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:Исходное неравенство сводится к совокупности двух систем неравенств.Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:x2 − 2x − 15 > 0Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:Парабола с ветвями вверх и нулями в точках -3 и 5Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.Почему эти методы неэффективны?Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:(x − 7)(x − 1)(x + 4)(x + 9) < 0Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.Что такое метод интерваловМетод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:
Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:Задача. Решите неравенство:(x − 2)(x + 7) < 0Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:(x − 2)(x + 7) = 0Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:x − 2 = 0 ⇒ x = 2;
Допустим, что число - бесконечная периодическая дробь. Тогда, начиная с -ой цифры, некоторая последовательность из цифр будет повторяться бесконечно. Очевидно, что, после -ой цифры найдутся ненулевые цифры. А значит искомый период длины содержит хотя бы одну ненулевую цифру.
Также очевидно, что в десятичной записи присутствует число . В нем одна 1, а за ней следуют нулей.
Пусть в период входят одна 1 и нулей этого числа. Но следующие цифр - нули (т.к. в предыдущее повторение периода вошло меньше, чем нулей, незадействованными остались подряд идущих нулей) - противоречие с тем, что в периоде есть ненулевая цифра.
А значит у дроби нет периода.
Т.к. она бесконечная (число натуральных чисел бесконечно), то иррациональная.
Непрерывная функция меняет знак только в тех точках, где она равна нулю. Такие точки разбивают координатную ось на куски, внутри которых знак функции никогда не меняется. Вот зачем мы решаем уравнение f (x) = 0 и отмечаем найденные корни на прямой. Найденные числа — это «пограничные» точки, отделяющие плюсы от минусов.
Чтобы выяснить знак функции на каком-либо интервале, достаточно подставить в функцию любое число из этого интервала. Например, для интервала (−5; 6) мы вправе брать x = −4, x = 0, x = 4 и даже x = 1,29374, если нам захочется. Почему это важно? Да потому что многих учеников начинают грызть сомнения. Мол, что если для x = −4 мы получим плюс, а для x = 0 — минус? А ничего — такого никогда не будет. Все точки на одномответ:
строгих неравенств
12 ноября 2017Материалы к урокуСкачать: [Домашнее задание] Домашнее заданиеСкачать: [ответы] ответыДля начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:(x − 5)(x + 3) > 0Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 < 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:Исходное неравенство сводится к совокупности двух систем неравенств.Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:x2 − 2x − 15 > 0Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:Парабола с ветвями вверх и нулями в точках -3 и 5Функция больше нуля там, где она проходит выше оси OX. В нашем случае это интервалы (−∞ −3) и (5; +∞) — это и есть ответ.Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.Почему эти методы неэффективны?Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:(x − 7)(x − 1)(x + 4)(x + 9) < 0Как решать такое неравенство? Перебирать все возможные комбинации плюсов и минусов? Да мы уснем быстрее, чем найдем решение. Рисовать график — тоже не вариант, поскольку непонятно, как ведет себя такая функция на координатной плоскости.Для таких неравенств нужен специальный алгоритм решения, который мы сегодня и рассмотрим.Что такое метод интерваловМетод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:
Решить уравнение f (x) = 0. Таким образом, вместо неравенства получаем уравнение, которое решается намного проще;
Отметить все полученные корни на координатной прямой. Таким образом, прямая разделится на несколько интервалов;
Выяснить знак (плюс или минус) функции f (x) на самом правом интервале. Для этого достаточно подставить в f (x) любое число, которое будет правее всех отмеченных корней;
Отметить знаки на остальных интервалах. Для этого достаточно запомнить, что при переходе через каждый корень знак меняется.
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f (x) > 0, или знаком «−», если неравенство имеет вид f (x) < 0.На первый взгляд может показаться, что метод интервалов — это какая-то жесть. Но на практике все будет очень просто. Стоит чуть-чуть потренироваться — и все станет понятно. Взгляните на примеры — и убедитесь в этом сами:Задача. Решите неравенство:(x − 2)(x + 7) < 0Работаем по методу интервалов. Шаг 1: заменяем неравенство уравнением и решаем его:(x − 2)(x + 7) = 0Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.
Допустим, что число - бесконечная периодическая дробь. Тогда, начиная с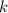
-ой цифры, некоторая последовательность из 
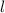цифр будет повторяться бесконечно. Очевидно, что, после 
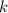-ой цифры найдутся ненулевые цифры. А значит искомый период длины 
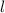содержит хотя бы одну ненулевую цифру.
Также очевидно, что в десятичной записи присутствует число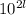
. В нем одна 1, а за ней следуют 
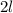нулей.
Пусть в период входят одна 1 и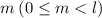
нулей этого числа. Но следующие 
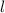цифр - нули (т.к. в предыдущее повторение периода вошло меньше, чем 
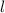нулей, незадействованными остались 
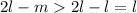подряд идущих нулей) - противоречие с тем, что в периоде есть ненулевая цифра.
А значит у дроби нет периода.
Т.к. она бесконечная (число натуральных чисел бесконечно), то иррациональная.
ответ: число иррационально