Слово «казак» известно с xiii[25]−xiv вв., оно впервые упоминается в словаре куманского (старокыпчакского) языка 1303 года. по одной из версий, слово «казак» тюркского происхождения. как пишет в. в. бартольд, оно происходит от слова «каз» (гусь), что в переносном смысле означает «вольный, как птица» и изначально применялось к человеку, в одиночку или с семьёй отделившемуся от своего государства, рода, и вынужденного самостоятельно искать средств содержания в степи , «вести жизнь искателя приключений». казаками могли называть недовольных правителем (ханом, царем или князем) подданных, ушедших в другое место, и самого правителя, потерпевшего поражение и оставшегося с небольшой группой сторонников. ту же этимологию имеет и название народа казахи.
Пусть лягушонок стартует в точке . Тогда, если какие-то две точки повторились, то лягушонок побывал также в точке дважды, т.е. мы попали в цикл. Если мы покажем, что уравнение имеет решение при любом , то цикл будет состоять из всех точек, и лягушонок побывает во всех точках по одному разу, а затем вернется в точку ;
Докажем для начала, что если существует решение для остатков , то существует решение для остатка . Это вполне очевидно: просто сложим два уравнения для остатков . Теперь, в частности, если существует решение для , то существует решение для всех остатков. То есть нам надо решить диофантово уравнение ; Для этого сразу положим ; Пусть ;
Тогда из числа нам нужно получить число ; Но мы умеем прибавлять единицу: . То есть ; Иными словами, получили решение , но нам нужно решение в натуральных числах. Не вопрос: добавим к 2020, а к добавим 99. Получим решение: .
Итак, план действий следующий.
Пусть мы находимся в точке . Прыгаем 41 раз на 100 и 1999 раз на 99. Теперь мы в точке . Таким образом, мы посетим все точки.
Пусть лягушонок стартует в точке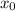 . Тогда, если какие-то две точки повторились, то лягушонок побывал также в точке
. Тогда, если какие-то две точки повторились, то лягушонок побывал также в точке 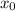 дважды, т.е. мы попали в цикл. Если мы покажем, что уравнение
дважды, т.е. мы попали в цикл. Если мы покажем, что уравнение 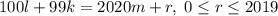 имеет решение при любом
имеет решение при любом  , то цикл будет состоять из всех точек, и лягушонок побывает во всех точках по одному разу, а затем вернется в точку
, то цикл будет состоять из всех точек, и лягушонок побывает во всех точках по одному разу, а затем вернется в точку 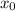 ;
;
Докажем для начала, что если существует решение для остатков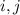 , то существует решение для остатка
, то существует решение для остатка 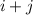 . Это вполне очевидно: просто сложим два уравнения для остатков
. Это вполне очевидно: просто сложим два уравнения для остатков 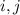 . Теперь, в частности, если существует решение для
. Теперь, в частности, если существует решение для 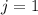 , то существует решение для всех остатков. То есть нам надо решить диофантово уравнение
, то существует решение для всех остатков. То есть нам надо решить диофантово уравнение 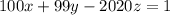 ; Для этого сразу положим
; Для этого сразу положим 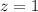 ; Пусть
; Пусть 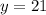 ;
;
Тогда из числа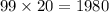 нам нужно получить число
нам нужно получить число 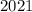 ; Но мы умеем прибавлять единицу:
; Но мы умеем прибавлять единицу: 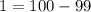 . То есть
. То есть 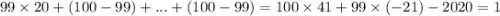 ; Иными словами, получили решение
; Иными словами, получили решение 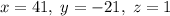 , но нам нужно решение в натуральных числах. Не вопрос: добавим к
, но нам нужно решение в натуральных числах. Не вопрос: добавим к 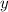 2020, а к
2020, а к  добавим 99. Получим решение:
добавим 99. Получим решение: 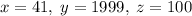 .
.
Итак, план действий следующий.
Пусть мы находимся в точке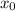 . Прыгаем 41 раз на 100 и 1999 раз на 99. Теперь мы в точке
. Прыгаем 41 раз на 100 и 1999 раз на 99. Теперь мы в точке 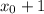 . Таким образом, мы посетим все точки.
. Таким образом, мы посетим все точки.