Пусть задуманное число х, составим уравнение и преобразуем его, чтобы проверить справедливость фокуса: ((110-(х+7)+15+х):2-9)*3=((110-х-7+15+х):2-9)*3=(59-9)*3=150 Как видно из преобразований значение выражения не зависит от задуманного числа.
2) Можно, если проходили отрицательные числа, если нет, то. х+7≤110 х≤103 Значит среди всех трехзначных чисел можно загадывать 100, 101, 102, 103. Чтобы загадывать любые числа, мы к 110 сначала прибавим задуманное число, а только потом отнимем. Получится такое условие:
Отгадай секрет следующего математического фокуса. задумай число и уменьши его на 7.К результату прибавь 110 и прибавь 15.От значения суммы отними задуманное число, результат подели пополам . от значения частного отними 9 и результат умножь на 3. ((110+(х-7)+15-х):2-9)*3=((110+х-7+15-х):2-9)*3=(59-9)*3=150
Предположим, что . Тогда и . Проверим последнее утверждение.
Данное произведение — это произведение трёх последовательных чисел, значит, один из множителей обязательно делится на 3. Так как p простое и больше 3, p-1 и p+1 чётны. Докажем, что произведение p-1 = 2k и p+1 = 2k+2 (k ∈ N) делится на 8:
. Оно, очевидно, делится на 4. Также оно делится ещё на 2, так как одно из чисел k и k+1 обязательно чётное.
.
Однако из этого не обязательно следует, что и . Но p > 3 и p — простое, значит, p не содержит множителей числа 24, то есть на 24 может делиться только , что и требовалось доказать.
((110-(х+7)+15+х):2-9)*3=((110-х-7+15+х):2-9)*3=(59-9)*3=150
Как видно из преобразований значение выражения не зависит от задуманного числа.
2) Можно, если проходили отрицательные числа, если нет, то.
х+7≤110
х≤103
Значит среди всех трехзначных чисел можно загадывать 100, 101, 102, 103.
Чтобы загадывать любые числа, мы к 110 сначала прибавим задуманное число, а только потом отнимем. Получится такое условие:
Отгадай секрет следующего математического фокуса. задумай число и уменьши его на 7.К результату прибавь 110 и прибавь 15.От значения суммы отними задуманное число, результат подели пополам . от значения частного отними 9 и результат умножь на 3.
((110+(х-7)+15-х):2-9)*3=((110+х-7+15-х):2-9)*3=(59-9)*3=150
Предположим, что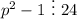
. Тогда и 
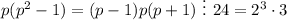. Проверим последнее утверждение.
Данное произведение — это произведение трёх последовательных чисел, значит, один из множителей обязательно делится на 3. Так как p простое и больше 3, p-1 и p+1 чётны. Докажем, что произведение p-1 = 2k и p+1 = 2k+2 (k ∈ N) делится на 8:
Однако из этого не обязательно следует, что и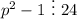
. Но p > 3 и p — простое, значит, p не содержит множителей числа 24, то есть на 24 может делиться только 
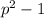, что и требовалось доказать.