(см. объяснение)
Пошаговое объяснение:
Поскольку в условии не дано основание логарифма, то примем его равным 10. При другом его численном значении логика решения не поменяется.
Первый :
Заметим, что если x - корень уравнения, то -x тоже. Тогда единственное решение возможно, если x=0.
При этом значении переменной найдем параметр:
Покажем, что при нем у уравнения нет других корней:
(здесь ОДЗ не пишем, так как преобразованиями оно гарантируется)
Тогда такое значение параметра подходит.
Второй :
Из этой строки следует, что условие всегда выполняется.
Решим параметр в координатах (x; a):
Выполним построение:
(см. прикрепленный файл)
Откуда следует, что ответом будет .
Задание выполнено!
(см. объяснение)
Пошаговое объяснение:
Поскольку в условии не дано основание логарифма, то примем его равным 10. При другом его численном значении логика решения не поменяется.
Первый :
Заметим, что если x - корень уравнения, то -x тоже. Тогда единственное решение возможно, если x=0.
При этом значении переменной найдем параметр:
Покажем, что при нем у уравнения нет других корней:
(здесь ОДЗ не пишем, так как преобразованиями оно гарантируется)
Тогда такое значение параметра подходит.
Второй :
Из этой строки следует, что условие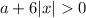 всегда выполняется.
всегда выполняется.
Решим параметр в координатах (x; a):
Выполним построение:
(см. прикрепленный файл)
Откуда следует, что ответом будет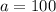 .
.
Задание выполнено!