Найдем уравнение прямой, параллельной касательной к графику функции .
Прямая, проходящая через точки A(x₁, y₁) и B(x₂, y₂), представляется уравнением . Подставляем все данные в условии значения и получаем:
(Отмечу, что уравнение можно было найти и без этого уравнения. Запишем уравнение в виде . Поскольку точки А и В принадлежат прямой, то выполняется система . Решая эту систему получаем, что , , т.е. уравнение прямой -
Угловой коэффициент заданной прямой равен коэффициенту перед x, т.е. 1. Поскольку у параллельных прямых угловые коэффициенты равны, то угловой коэффициент касательной также равен 1.
Хотя бы две = кубики с 2,3 закрашенными гранями.
Кубиков с тремя гранями = 4 (верхние углы куба)
Кубики с двумя гранями (нижние углы куба) = 4
Остальные - кубики с двумя гранями - ребра = 32-4-4=24
По факту у нас получается 8 ребер - 4 ребра верхней грани куба, 4 ребра боковых.
24:8=3 кубика в ребре.
Получаем что у нас куб размерами 5х5х5 = всего 125 куб, облит краской.
Покрашенных кубиков: с 2 и 3 гранями - всего 32
С 1 гранью: 3*3+4*4*3 = 57
Остальные - без окрашенных граней: 125 - 32 - 57 = 36
Проверка: если убрать все окрашенные кубики, то останется параллепипед размерами 3х3х4 = 36
Найдем уравнение прямой, параллельной касательной к графику функции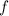
.
Прямая, проходящая через точки A(x₁, y₁) и B(x₂, y₂), представляется уравнением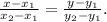
. Подставляем все данные в условии значения и получаем:
(Отмечу, что уравнение можно было найти и без этого уравнения. Запишем уравнение в виде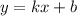
. Поскольку точки А и В принадлежат прямой, то выполняется система 
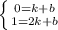. Решая эту систему получаем, что 
, 
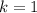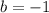, т.е. уравнение прямой -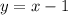 
Угловой коэффициент заданной прямой равен коэффициенту перед x, т.е. 1. Поскольку у параллельных прямых угловые коэффициенты равны, то угловой коэффициент касательной также равен 1.
ОТВЕТ: 1.